- Graph of the constraints in xy-plane needed to be drawn.
- The two constraints are given by $3 x+4 y \leq 60$ and $5 x-3 y \leq 20$.
- To draw $3 x+4 y \leq 60$, by putting $x=0$, we get $y=15$. Subsequently putting $y=0$ gives $x=20$.
- Two points obtained are $(0,15)$ and $(20,0)$. Joining these points and extending the line on both sides will give the line $3 x+4 y \leq 60$.
- Similarly, $5 x-3 y \leq 20$ will be drawn.
- Based on the inequalities, the feasible region is obtained which is shown in red color in the figure below:


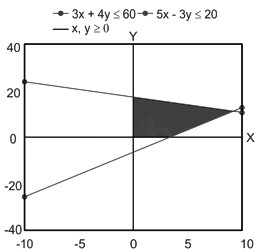
- Now the corner points need to be determined.
- First corner point will be the origin $(0,0)$.
- Second corner point is the point where $3 x+4 y \leq 60$ intersects the $y$-axis. Putting $x=0$, we get the first corner point as $(0,15)$.
- Third corner point is the point where $5 x-3 y \leq 20$ intersects the $x$-axis. Putting $y=0$, we get the first corner point as $(4,0)$.
- Fourth corner point will be the intersection of two inequalities. Solving them we get, $y=\frac{240}{29}$ and $x=\frac{260}{29}$.
- Below is the table showing the corner points and the value of the objective functions at those points.
$\begin{array}{|l|l|l|} \hline \text{Sr. No.} & \text{Corner Points} & Z=30 x- 18 y \\ \hline 1 & (0,0) & 0 \\ \hline 2 & (0,15) & -270 \\ \hline 3 & (4,0) & 120 \\ \hline 4 & \left(\frac{260}{29}, \frac{240}{29}\right) & 120 \\ \hline \end{array}$
- The table indicates that the objective function has a maximum value at $(4,0)$ and $\left(\frac{260}{29}, \frac{240}{29}\right)$.
- Hence, the maximum value of the function lies on any point on the line joining the points $(4,0)$ and $\left(\frac{260}{29}, \frac{240}{29}\right.$ ).
- There will infinite number of points on the line where the value of the objective function will be maximum.