Search any question & find its solution
Question:
Answered & Verified by Expert
A liquid is allowed to flow into a tube of truncated cone shape. Identify the correct statement from the following.
Options:
Solution:
2067 Upvotes
Verified Answer
The correct answer is:
The speed is low at the wider end and high at the narrow end.
The theorem of continuity is valid.
$$
\therefore \mathrm{A}_{1} \mathrm{v}_{1} \rho=\mathrm{A}_{2} \mathrm{v}_{2} \rho
$$
As the density of the liquid can be taken as uniform.
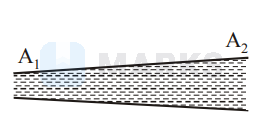
$\therefore \mathrm{A}_{1} \mathrm{v}_{1}=\mathrm{A}_{2} \mathrm{v}_{2}$
$\Rightarrow$ Smaller the area, greater the velocity.
$$
\therefore \mathrm{A}_{1} \mathrm{v}_{1} \rho=\mathrm{A}_{2} \mathrm{v}_{2} \rho
$$
As the density of the liquid can be taken as uniform.

$\therefore \mathrm{A}_{1} \mathrm{v}_{1}=\mathrm{A}_{2} \mathrm{v}_{2}$
$\Rightarrow$ Smaller the area, greater the velocity.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.