Search any question & find its solution
Question:
Answered & Verified by Expert
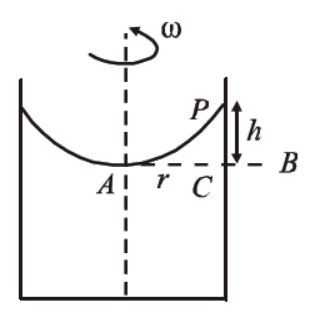
A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $r$ and angular velocity of rotation is $\omega$, then the difference in the heights of the liquid at the centre of the vessel and the edge is
Options:
Solution:
2573 Upvotes
Verified Answer
The correct answer is:
$\frac{r^2 \omega^2}{2 g}$
From Bernoulli's theorem,
$$
P_A+\frac{1}{2} d v_A^2+d g h_A=P_B+\frac{1}{2} d v_B^2+d g h_B
$$
Here, $h_A=h_B$
$$
\begin{aligned}
& \therefore P_A+\frac{1}{2} d v_A^2=P_B+\frac{1}{2} d v_B^2 \\
& P_A-P_B=\frac{1}{2} d\left[v_B^2-v_A^2\right] \\
& \text { Now, } v_A=0, \quad v_B=r \omega \\
& \text { and } P_A-P_B=h d g
\end{aligned}
$$
$\therefore h d g=\frac{1}{2} d r^2 \omega^2$ or $h=\frac{r^2 \omega^2}{2 g}$
$$
P_A+\frac{1}{2} d v_A^2+d g h_A=P_B+\frac{1}{2} d v_B^2+d g h_B
$$
Here, $h_A=h_B$
$$
\begin{aligned}
& \therefore P_A+\frac{1}{2} d v_A^2=P_B+\frac{1}{2} d v_B^2 \\
& P_A-P_B=\frac{1}{2} d\left[v_B^2-v_A^2\right] \\
& \text { Now, } v_A=0, \quad v_B=r \omega \\
& \text { and } P_A-P_B=h d g
\end{aligned}
$$
$\therefore h d g=\frac{1}{2} d r^2 \omega^2$ or $h=\frac{r^2 \omega^2}{2 g}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.