The charge $+q$ spreads uniformly on the outer surface of $A$ and $-q$ uniformly spreads on the inner surface of $\mathrm{B}$. An electric field $\overrightarrow{\mathrm{E}}$ is produced between the two shells which will be directed radially outwards as shown in Fig.


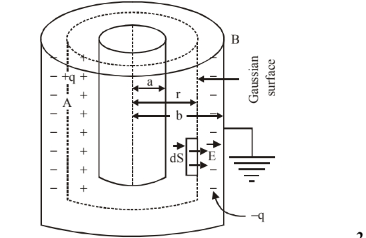
Let us consider a coaxial cylindrical Gaussian surface of radius $r$. The electric flux through this cylindrical Gaussian surface is given by
$$
\begin{aligned}
\phi_{\mathrm{E}} &=\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{s}}=\int \mathrm{EdS} \cos 0^{\circ} \\
&=\mathrm{E} \int \mathrm{dS}=\mathrm{E}(2 \pi \mathrm{r} \ell)
\end{aligned}
$$
The flux through the end faces of the Gaussian cylinder is zero because $\overrightarrow{\mathrm{E}}$ is parallel to them. Hence $\phi_{\mathrm{E}}$ is the flux through whole of the Gaussian surface.
Applying Gauss's law, $\mathrm{E} \times 2 \pi \mathrm{r} \ell=\frac{\mathrm{q}}{\varepsilon_0}$
or $\quad E=\frac{1}{2 \pi \varepsilon_0 \ell} \cdot \frac{q}{r}$
or $\quad E=\frac{1}{2 \pi \varepsilon_0 \mathrm{r}} \cdot \frac{\mathrm{q}}{\ell}=\frac{1}{2 \pi \varepsilon_0 \mathrm{r}} \cdot \lambda$