Search any question & find its solution
Question:
Answered & Verified by Expert
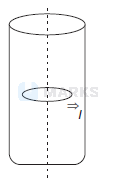
A long circular tube of length $10 \mathrm{~m}$ and radius $0.3 \mathrm{~m}$ carries a current I along its curved surface as shown. A wire loop of resistance $0.005 \Omega$ and of radius $0.1 \mathrm{~m}$ is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $I=I_0 \cos 300 t$, where $I_0$ is constant. If the magnetic moment of the loop is $N \mu_0 I_0 \sin 300 t$, then $N$ is

Solution:
1002 Upvotes
Verified Answer
The correct answer is:
6
Take the circular tube as a long solenoid. The wires are closely wound. Magnetic field inside the solenoid is
$$
B=\mu_0 n i
$$
Here, $n=$ number of turns per unit length
$\therefore n i=$ current per unit length
In the given problem,
$$
\begin{aligned}
& n i=\frac{I}{L} \\
\therefore \quad B & =\frac{\mu_0 I}{L}
\end{aligned}
$$
Flux passing through the circular coil is
$$
\phi=B S=\left(\frac{\mu_0 I}{L}\right)\left(\pi r^2\right)
$$
Induced emf, $e=-\frac{d \phi}{d t}=-\left(\frac{\mu_0 \pi r^2}{L R}\right) \cdot \frac{d I}{d t}$
Induced current,
$$
i=\frac{e}{R}=-\left(\frac{\mu_0 \pi r^2}{L R}\right) \frac{d I}{d t}
$$
Magnetic moment $i A=i \pi r^2$
or $\quad M=-\left(\frac{\mu_0 \pi^2 r^4}{L R}\right) \cdot \frac{d I}{d t}$
Given, $\quad I=I_0 \cos 300 t$
$$
\therefore \quad \frac{d I}{d t}=-300 I_0 \sin (300 t)
$$
Substituting in Eq. (i), we get
$$
\begin{aligned}
M & =\left(\frac{300 \pi^2 r^4}{L R}\right) \mu_0 I_0 \sin 300 t \\
\therefore \quad N & =\frac{300 \pi^2 r^4}{L R}
\end{aligned}
$$
Substituting the values, we get
$$
\begin{aligned}
N & =\frac{300(22 / 7)^2(0.1)^4}{(10)(0.005)} \\
& =5.926
\end{aligned}
$$
or $\quad N \simeq 6$
Analysis of Question
Question is difficult to understand inside the examination hall. But 5 to $10 \%$ question in IIT JEE are always difficult. Students should not panic. Because topper of IIT JEE scores approximately $80-90 \%$.
$$
B=\mu_0 n i
$$
Here, $n=$ number of turns per unit length
$\therefore n i=$ current per unit length
In the given problem,
$$
\begin{aligned}
& n i=\frac{I}{L} \\
\therefore \quad B & =\frac{\mu_0 I}{L}
\end{aligned}
$$
Flux passing through the circular coil is
$$
\phi=B S=\left(\frac{\mu_0 I}{L}\right)\left(\pi r^2\right)
$$
Induced emf, $e=-\frac{d \phi}{d t}=-\left(\frac{\mu_0 \pi r^2}{L R}\right) \cdot \frac{d I}{d t}$
Induced current,
$$
i=\frac{e}{R}=-\left(\frac{\mu_0 \pi r^2}{L R}\right) \frac{d I}{d t}
$$
Magnetic moment $i A=i \pi r^2$
or $\quad M=-\left(\frac{\mu_0 \pi^2 r^4}{L R}\right) \cdot \frac{d I}{d t}$
Given, $\quad I=I_0 \cos 300 t$
$$
\therefore \quad \frac{d I}{d t}=-300 I_0 \sin (300 t)
$$
Substituting in Eq. (i), we get
$$
\begin{aligned}
M & =\left(\frac{300 \pi^2 r^4}{L R}\right) \mu_0 I_0 \sin 300 t \\
\therefore \quad N & =\frac{300 \pi^2 r^4}{L R}
\end{aligned}
$$
Substituting the values, we get
$$
\begin{aligned}
N & =\frac{300(22 / 7)^2(0.1)^4}{(10)(0.005)} \\
& =5.926
\end{aligned}
$$
or $\quad N \simeq 6$
Analysis of Question
Question is difficult to understand inside the examination hall. But 5 to $10 \%$ question in IIT JEE are always difficult. Students should not panic. Because topper of IIT JEE scores approximately $80-90 \%$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.