Search any question & find its solution
Question:
Answered & Verified by Expert
A long cylindrical pipe of radius $20 \mathrm{~cm}$ is closed at its upper end and has an airtight piston of negligible mass as shown. When a $50 \mathrm{Kg}$ mass is attached to the other end of the pistion, it moves down by a distance $\Delta /$ before coming to equilibrium. Assuming air to be an ideal gas, $\Delta / \mathrm{L}$ (see figure) is close to $\left(\mathrm{g}=10 \mathrm{~ms}^{2}\right.$, atmospheric pressure is $10^{5}$ Pascal),
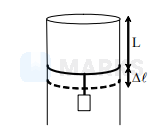
Options:

Solution:
2963 Upvotes
Verified Answer
The correct answer is:
$0.04$
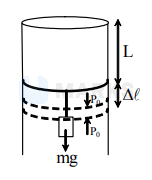
Process is isothermal
$\begin{array}{l}
\mathrm{P}_{1} \mathrm{~V}_{1}=\mathrm{P}_{2} \mathrm{~V}_{2} \\
\left(\mathrm{P}_{0}\right)(\mathrm{A})(\ell) \Rightarrow \mathrm{PA}(\ell+\Delta \ell) \\
\mathrm{P}_{\mathrm{final}} \Rightarrow \frac{\mathrm{P}_{0} \mathrm{~A} \ell}{\mathrm{A}(\ell+\Delta \ell)} \Rightarrow \frac{\mathrm{P}_{0} \ell}{\ell+\Delta \ell}
\end{array}$
By force equilibrium
$\begin{array}{l}
\left(P_{0}-P\right) A \Rightarrow m g \\
\left(P_{0}-\frac{P_{0} \ell}{\ell+\Delta \ell}\right) A=m g \\
\frac{\Delta \ell}{\ell} \approx 0.04
\end{array}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.