Search any question & find its solution
Question:
Answered & Verified by Expert
A man in a car at location Q on a straight highway is moving with speed $\mathrm{v}$. He decides to reach a point $P$ in a field at a distance $d$ from highway (point $M$ ) as shown in the figure.Speed of the car in the field is half to that on the highway. What should be the distance RM, so that the time taken to reach $P$ is minimum?
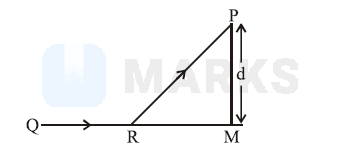
Options:

Solution:
2247 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{d}}{\sqrt{3}}$
$\frac{\mathrm{d}}{\sqrt{3}}$
Let the car turn of the highway at a distance ' $x$ ' from the point $\mathrm{M}$. So, $\mathrm{RM}=x$ And if speed of car in field is $v$, then time taken by the car to cover the distance $Q R=$ $Q M-x$ on the highway,
$$
t_1=\frac{Q M-x}{2 v}
$$
Time taken to travel the distance ' $R P^{\prime}$ in the field
$$
t_2=\frac{\sqrt{d^2+x^2}}{v}
$$
Total time elapsed to move the car from $Q$ to $P$
$$
t=t_1+t_2=\frac{Q M-x}{2 v}+\frac{\sqrt{d^2+x^2}}{v}
$$
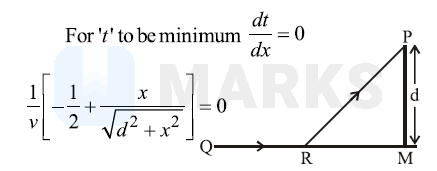
$$
\text { or } x=\frac{d}{\sqrt{2^2-1}}=\frac{d}{\sqrt{3}}
$$
$$
t_1=\frac{Q M-x}{2 v}
$$
Time taken to travel the distance ' $R P^{\prime}$ in the field
$$
t_2=\frac{\sqrt{d^2+x^2}}{v}
$$
Total time elapsed to move the car from $Q$ to $P$
$$
t=t_1+t_2=\frac{Q M-x}{2 v}+\frac{\sqrt{d^2+x^2}}{v}
$$
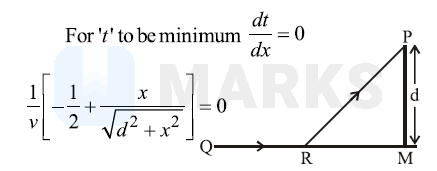
$$
\text { or } x=\frac{d}{\sqrt{2^2-1}}=\frac{d}{\sqrt{3}}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.