Search any question & find its solution
Question:
Answered & Verified by Expert
A mass $M$ is tied to the top of two identical poles of height $H$ using massless strings of equal length. The mass is at height $h$ above the ground at equilibrium. If the distance between poles is $L$ the tension in each string will be
Options:
Solution:
2998 Upvotes
Verified Answer
The correct answer is:
$\frac{M g \sqrt{\left(\frac{L}{2}\right)^2+(H-h)^2}}{2(H-h)}$
At equilibrium, $M g=2 T \sin \theta$
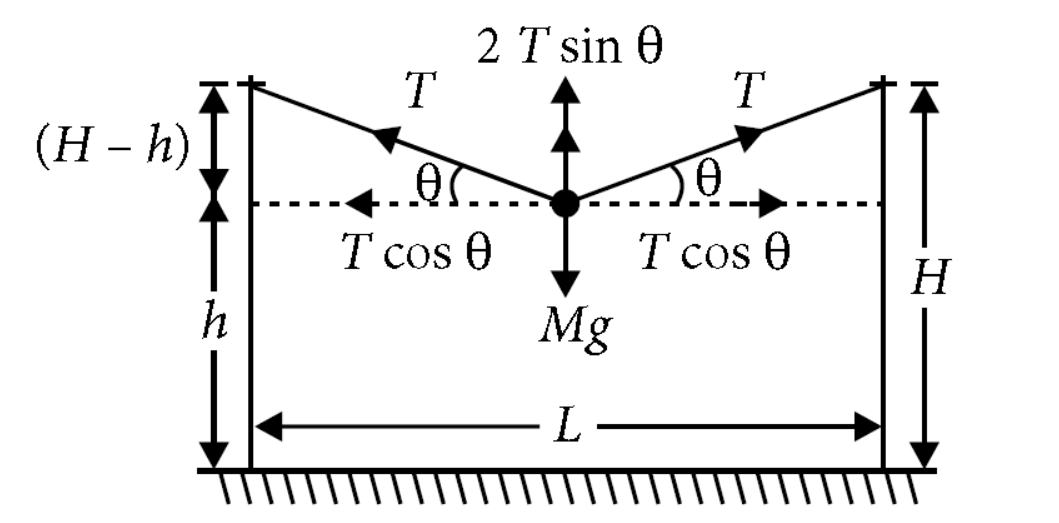
$T=\frac{M g}{2 \sin \theta}$
Here, $\sin \theta=\frac{(H-h)}{\sqrt{(L / 2)^2+(H-h)^2}}$
From equation (i)
$$
T=\frac{M g \sqrt{(L / 2)^2+(H-h)^2}}{2(H-h)}
$$

$T=\frac{M g}{2 \sin \theta}$
Here, $\sin \theta=\frac{(H-h)}{\sqrt{(L / 2)^2+(H-h)^2}}$
From equation (i)
$$
T=\frac{M g \sqrt{(L / 2)^2+(H-h)^2}}{2(H-h)}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.