Search any question & find its solution
Question:
Answered & Verified by Expert
A mass of $2.9 \mathrm{~kg}$ is suspended from a string of length $50 \mathrm{~cm}$ and is at rest. Another body of mass $100 \mathrm{~g}$, which is moving horizontally with a velocity of $150 \mathrm{~m} / \mathrm{s}$ strikes and sticks to it. Subsequently when the string makes an angle of $60^{\circ}$ with the vertical, the tension in the string is $\left(g=10 \mathrm{~m} / \mathrm{s}^2\right)$
Options:
Solution:
1062 Upvotes
Verified Answer
The correct answer is:
135 N
From law of conservation of momentum, we known,
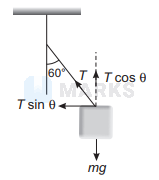
$$
\begin{array}{lc}
& m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \\
u_1=0, u_2=150 \mathrm{~m} / \mathrm{s}, m_1=2.9 \mathrm{~kg} \text { and } m_2=0.1 \mathrm{~kg} \\
\text { So, } & 2.9 \times 150=(2.9+0.1) \mathrm{v} \\
\Rightarrow & \frac{2.9 \times 150}{3}=v \\
\Rightarrow & \\
\text { Also, } & T \sin \theta=\frac{m v^2}{r}
\end{array}
$$
Putting the values and solving, we get $T=135 \mathrm{~N}$.

$$
\begin{array}{lc}
& m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \\
u_1=0, u_2=150 \mathrm{~m} / \mathrm{s}, m_1=2.9 \mathrm{~kg} \text { and } m_2=0.1 \mathrm{~kg} \\
\text { So, } & 2.9 \times 150=(2.9+0.1) \mathrm{v} \\
\Rightarrow & \frac{2.9 \times 150}{3}=v \\
\Rightarrow & \\
\text { Also, } & T \sin \theta=\frac{m v^2}{r}
\end{array}
$$
Putting the values and solving, we get $T=135 \mathrm{~N}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.