Search any question & find its solution
Question:
Answered & Verified by Expert
A mild steel wire of length $2 L$ and cross-sectional area $A$ is stretched, well within elastic limit, horizontally between two pillars (figure). A mass $m$ is suspended from the midpoint of the wire. Strain in the wire is
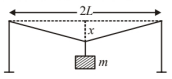
Options:

Solution:
2801 Upvotes
Verified Answer
The correct answer is:
$\frac{x^2}{2 L^2}$
$\frac{x^2}{2 L^2}$
Consider the given diagram
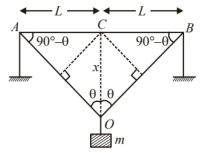
So, change in length
$$
\begin{aligned}
\Delta L &=\left(A_0+B_0\right)-(A C+C B) \\
&=2 B O-2 A C \\
&=2[B O-A C](\therefore \mathrm{AO}=\mathrm{BO}, \mathrm{AC}=\mathrm{CB}) \\
&=2\left[\left(x^2+L^2\right)^{1 / 2}-L\right]=2 L\left[\left(1+\frac{x^2}{L^2}\right)^{1 / 2}-1\right]
\end{aligned}
$$
$\Delta L=2 L\left[1+\frac{1}{2} \frac{x^2}{L^2}-1\right]=\frac{x^2}{L} \quad[\because x \ll L]$
Strain $=\frac{\Delta L}{2 L}=\frac{x^2 / L}{2 L}=\frac{x^2}{2 L^2}$

So, change in length
$$
\begin{aligned}
\Delta L &=\left(A_0+B_0\right)-(A C+C B) \\
&=2 B O-2 A C \\
&=2[B O-A C](\therefore \mathrm{AO}=\mathrm{BO}, \mathrm{AC}=\mathrm{CB}) \\
&=2\left[\left(x^2+L^2\right)^{1 / 2}-L\right]=2 L\left[\left(1+\frac{x^2}{L^2}\right)^{1 / 2}-1\right]
\end{aligned}
$$
$\Delta L=2 L\left[1+\frac{1}{2} \frac{x^2}{L^2}-1\right]=\frac{x^2}{L} \quad[\because x \ll L]$
Strain $=\frac{\Delta L}{2 L}=\frac{x^2 / L}{2 L}=\frac{x^2}{2 L^2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.