Search any question & find its solution
Question:
Answered & Verified by Expert
A mild wire of steel of length $1 \mathrm{~m}$ and cross-sectional area $0.5 \times 10^{-2} \mathrm{~cm}^2$ is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 $\mathrm{g}$ is suspended from the mid point of the wire. Calculate the depression of the mid point. $g=10 \mathrm{~m} /$ $\mathrm{s}^2, Y=2 \times 10^{11} \mathrm{~N} / \mathrm{m}^2$ $s^2, Y=2 \times 10^{11} \mathrm{~N} / \mathrm{m}^2$ Let $x$ be the depression of the mid point
Solution:
2517 Upvotes
Verified Answer
Let $x$ be the depression of the mid point
$$
\begin{aligned}
&\therefore \quad \text { From the figure, } \mathrm{AC}=\mathrm{CB}=l=0.5 \mathrm{~m} \\
&m=100 \mathrm{~g}=0.1 \mathrm{~kg} \\
&\mathrm{CD}=x, \mathrm{AD}=\mathrm{BD}=\sqrt{l^2+x^2}
\end{aligned}
$$
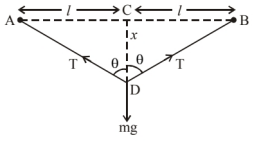
Increase in length, $\Delta l=\mathrm{AD}+\mathrm{DB}-\mathrm{AB}$ $=2 \mathrm{AD}-\mathrm{AB}$
$\Delta l=2 \sqrt{l^2+x^2}-2 l$
$$
=2 l\left(1+\frac{x^2}{l^2}\right)^{1 / 2}-2 l=2 l\left(1+\frac{x^2}{2 l^2}\right)-2 l
$$
(expanding binomially and neglecting higher powers of $x^2 / l^2$ as $\left.x < l\right)$
$$
\Rightarrow \Delta l=2 l+\frac{x^2}{2 l^2} \times 2 l-2 l=\frac{x^2}{l}
$$
Strain $=\frac{\Delta l}{2 l}=\frac{x^2 / l}{2 l}=\frac{x^2}{2 l^2}$
Let $\mathrm{T}$ be the tension in the string
$\therefore \quad 2 \mathrm{~T} \cos \theta=\mathrm{mg} \Rightarrow \mathrm{T}=\frac{\mathrm{mg}}{2 \cos \theta}$
$\cos \theta=\frac{x}{\sqrt{l^2+x^2}}=\frac{x}{l\left(1+\frac{x^2}{l^2}\right)^{1 / 2}}$
$=\frac{x}{l\left(1+\frac{x^2}{2 l^2}\right)}$
As $x \ll l, 1+\frac{x^2}{2 l^2} \approx 1 \quad \therefore \cos \theta=\frac{x}{l}$
$\therefore \mathrm{T}=\frac{m g}{2(x / l)}=\frac{m g l}{2 x}$ and stress $=\frac{\mathrm{T}}{\mathrm{A}}=\frac{m g l}{2 A x}$
$Y=\frac{\text { stress }}{\text { strain }}=\frac{m g l}{2 \mathrm{Ax}} \times \frac{2 l^2}{x^2}=\frac{m g l^3}{\mathrm{~A} x^3}$
$\therefore x=l\left[\frac{m g}{Y A}\right]^{1 / 3}$
$=0.5\left[\frac{0.1 \times 10}{2 \times 10^{11} \times 0.5 \times 10^{-6}}\right]^{1 / 3}$
$=1.074 \times 10^{-2} \mathrm{~m}$
$$
\begin{aligned}
&\therefore \quad \text { From the figure, } \mathrm{AC}=\mathrm{CB}=l=0.5 \mathrm{~m} \\
&m=100 \mathrm{~g}=0.1 \mathrm{~kg} \\
&\mathrm{CD}=x, \mathrm{AD}=\mathrm{BD}=\sqrt{l^2+x^2}
\end{aligned}
$$

Increase in length, $\Delta l=\mathrm{AD}+\mathrm{DB}-\mathrm{AB}$ $=2 \mathrm{AD}-\mathrm{AB}$
$\Delta l=2 \sqrt{l^2+x^2}-2 l$
$$
=2 l\left(1+\frac{x^2}{l^2}\right)^{1 / 2}-2 l=2 l\left(1+\frac{x^2}{2 l^2}\right)-2 l
$$
(expanding binomially and neglecting higher powers of $x^2 / l^2$ as $\left.x < l\right)$
$$
\Rightarrow \Delta l=2 l+\frac{x^2}{2 l^2} \times 2 l-2 l=\frac{x^2}{l}
$$
Strain $=\frac{\Delta l}{2 l}=\frac{x^2 / l}{2 l}=\frac{x^2}{2 l^2}$
Let $\mathrm{T}$ be the tension in the string
$\therefore \quad 2 \mathrm{~T} \cos \theta=\mathrm{mg} \Rightarrow \mathrm{T}=\frac{\mathrm{mg}}{2 \cos \theta}$
$\cos \theta=\frac{x}{\sqrt{l^2+x^2}}=\frac{x}{l\left(1+\frac{x^2}{l^2}\right)^{1 / 2}}$
$=\frac{x}{l\left(1+\frac{x^2}{2 l^2}\right)}$
As $x \ll l, 1+\frac{x^2}{2 l^2} \approx 1 \quad \therefore \cos \theta=\frac{x}{l}$
$\therefore \mathrm{T}=\frac{m g}{2(x / l)}=\frac{m g l}{2 x}$ and stress $=\frac{\mathrm{T}}{\mathrm{A}}=\frac{m g l}{2 A x}$
$Y=\frac{\text { stress }}{\text { strain }}=\frac{m g l}{2 \mathrm{Ax}} \times \frac{2 l^2}{x^2}=\frac{m g l^3}{\mathrm{~A} x^3}$
$\therefore x=l\left[\frac{m g}{Y A}\right]^{1 / 3}$
$=0.5\left[\frac{0.1 \times 10}{2 \times 10^{11} \times 0.5 \times 10^{-6}}\right]^{1 / 3}$
$=1.074 \times 10^{-2} \mathrm{~m}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.