Search any question & find its solution
Question:
Answered & Verified by Expert
A mirror in the first quadrant is in the shape of a hyperbola whose equation is $\mathrm{xy}$ $=1 .$ A light source in the second quadrant emits a beam of light that hits the mirror at the point $(2,1 / 2)$. If the reflected ray is parallel to the $\mathrm{y}$-axis the slope of the incident beam is
Options:
Solution:
2691 Upvotes
Verified Answer
The correct answer is:
$\frac{15}{8}$
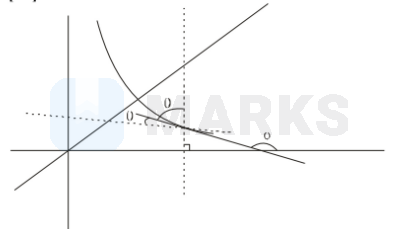
Slope of tangent at $\left(2, \frac{1}{2}\right)$
$$
\begin{array}{l}
\mathrm{m}=-\frac{1}{4} \\
\tan \theta=-\frac{1}{\mathrm{y}} \\
\theta=\phi-90^{\circ} \\
\tan \theta=4
\end{array}
$$
Slope of incident ray $=\mathrm{m}$
$$
\begin{array}{l}
\left|\frac{m-\left(-\frac{1}{4}\right)}{1+m\left(-\frac{1}{4}\right)}\right|=\tan \theta=4 \\
\left|\frac{4 m+1}{4-m}\right|=4 \\
4 m+1=16-4 m \\
m=\frac{15}{8}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.