Search any question & find its solution
Question:
Answered & Verified by Expert
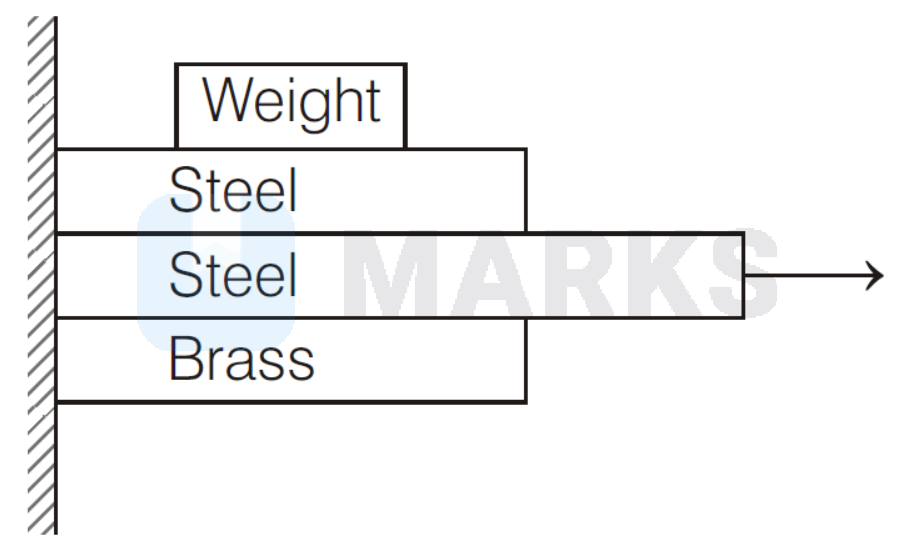
A movable steel plate is placed between fixed steel and brass plates and the stack of plates is
subjected to a weight of $100 \mathrm{~N}$ as shown in the figure. The coefficient of kinetic friction for steel on steel
is 0.57 and for steel on brass is 0.44 . Assuming that the entire weight comes onto the stack and that the weight of the plates is negligible in comparison to the applied weight, the force required to move the middle plate (in $\mathrm{N}$ ) is
Options:
subjected to a weight of $100 \mathrm{~N}$ as shown in the figure. The coefficient of kinetic friction for steel on steel
is 0.57 and for steel on brass is 0.44 . Assuming that the entire weight comes onto the stack and that the weight of the plates is negligible in comparison to the applied weight, the force required to move the middle plate (in $\mathrm{N}$ ) is

Solution:
1354 Upvotes
Verified Answer
The correct answer is:
101
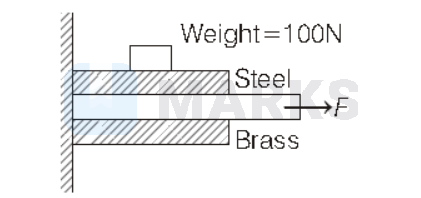
For given figure,
$\mu_{S S}=$ coefficient of friction between steel and steel $=0.57$
and $\mu_{S B}=$ coefficient of friction between steel and brass $=0.44$.
$$
\text { Free body diagram }
$$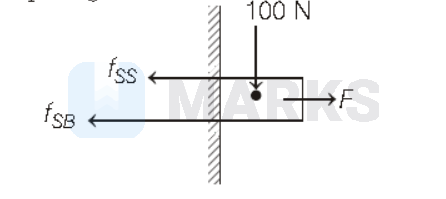
where, $f_{S S}=$ friction between steel plates and $f_{S B}=$ friction between steel and brass plates. $\Rightarrow$ For kinetic-friction, the applied force $(F)$ is equal or greater than friction force for moving the steel plate, so $f_{S S}+f_{S B} \leq F$
Therefore,
$$
\begin{aligned}
& f_{S S}=\mu_{S S} \times R=0.57 \times 100=57 \mathrm{~N} \\
& f_{S B}=\mu_{S B} \times R=0.44 \times 100=44 \mathrm{~N} \\
& 57+44=N \\
& \Rightarrow \quad 101 \text { newton }=N \\
&
\end{aligned}
$$
$$
$\mu_{S S}=$ coefficient of friction between steel and steel $=0.57$
and $\mu_{S B}=$ coefficient of friction between steel and brass $=0.44$.

$$
\text { Free body diagram }
$$

where, $f_{S S}=$ friction between steel plates and $f_{S B}=$ friction between steel and brass plates. $\Rightarrow$ For kinetic-friction, the applied force $(F)$ is equal or greater than friction force for moving the steel plate, so $f_{S S}+f_{S B} \leq F$
Therefore,
$$
\begin{aligned}
& f_{S S}=\mu_{S S} \times R=0.57 \times 100=57 \mathrm{~N} \\
& f_{S B}=\mu_{S B} \times R=0.44 \times 100=44 \mathrm{~N} \\
& 57+44=N \\
& \Rightarrow \quad 101 \text { newton }=N \\
&
\end{aligned}
$$
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.