Search any question & find its solution
Question:
Answered & Verified by Expert
A network of resistances, cell and capacitor $\mathrm{C}(=2 \mu \mathrm{F})$ is shown in adjoining figure.In steady state condition, the charge on $2 \mu \mathrm{F}$ capacitor is $Q$, while $R$ is unknown resistance. Values of $Q$ and $R$ are respectively
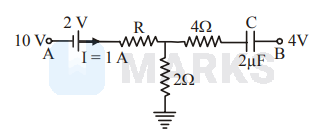
Options:

Solution:
2332 Upvotes
Verified Answer
The correct answer is:
$4 \mu \mathrm{C}$ and $10 \Omega$
In the steady state, current through capacitor
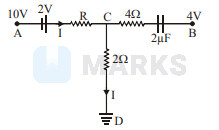
Using Kirchhof's voltage law to the circuit ACD
We have, $10-2+1 \times \mathrm{R}+1 \times 2=0$ or $\mathrm{R}=10 \Omega$
Potential difference across $\mathrm{C}$ and $\mathrm{D}$
$\mathrm{V}_{\mathrm{C}}-\mathrm{V}_{\mathrm{D}}=2 \times 1=2 \mathrm{~V}$
As $\mathrm{V}_{\mathrm{D}}=0 \mathrm{~V}$
So, $V_{C}=2 V$
Potential difference across capacitor $=4-2=2 \mathrm{~V}$
$\therefore$ Chargeon capacitor $\mathrm{Q}=\mathrm{CV}=2 \mu \mathrm{F} \times 2=4 \mu \mathrm{C}$

Using Kirchhof's voltage law to the circuit ACD
We have, $10-2+1 \times \mathrm{R}+1 \times 2=0$ or $\mathrm{R}=10 \Omega$
Potential difference across $\mathrm{C}$ and $\mathrm{D}$
$\mathrm{V}_{\mathrm{C}}-\mathrm{V}_{\mathrm{D}}=2 \times 1=2 \mathrm{~V}$
As $\mathrm{V}_{\mathrm{D}}=0 \mathrm{~V}$
So, $V_{C}=2 V$
Potential difference across capacitor $=4-2=2 \mathrm{~V}$
$\therefore$ Chargeon capacitor $\mathrm{Q}=\mathrm{CV}=2 \mu \mathrm{F} \times 2=4 \mu \mathrm{C}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.