Search any question & find its solution
Question:
Answered & Verified by Expert
A non-conducting disc of radius $R$ has surface charge density which varies with distance from the centre as $\sigma(r)=\sigma_0\left[1+\sqrt{\frac{r}{R}}\right]$, where $\sigma_0$ is a constant. The disc rotates about its axis with angular velocity $\omega$. If $B$ is the magnitude of magnetic induction at the centre, then $\frac{B}{\mu_0 \sigma_0 \omega R}$ will be
Options:
Solution:
2755 Upvotes
Verified Answer
The correct answer is:
$\frac{5}{6}$
Consider an elemental ring of radius $r$ of thickness $d r$
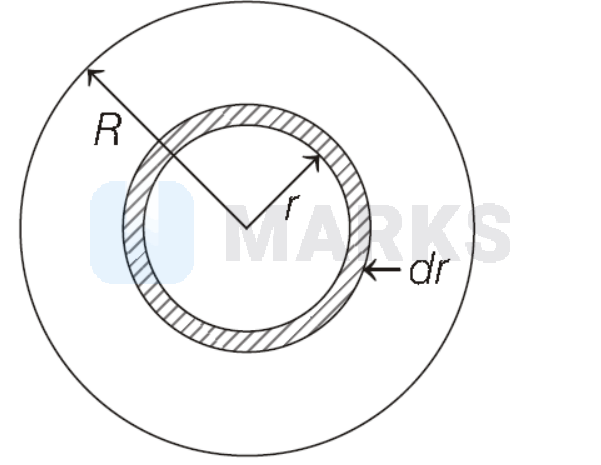
Charge on ring $d q=$ Area of ring $\times$ Charge density $\Rightarrow \quad d q=(2 \pi r \cdot d r) \sigma$
$\Rightarrow$ Current through ring, $d i=\frac{d q}{T}$, as angular velocity of disc is $\omega$.
So, $\quad \frac{2 \pi}{\omega}=T$
$\Rightarrow \quad d i=\frac{\omega d q}{2 \pi}=\frac{\omega(2 \pi r \cdot d r) \sigma}{2 \pi}=\omega r \sigma d r$
Now, magnetic induction due to elemental ring at the centre,
$$
d B=\frac{\mu_0 d i}{2 r}=\frac{\mu_0 \operatorname{\omega or} \sigma}{2 r} \cdot d r=\frac{\mu_0 \omega \sigma}{2} \cdot d r
$$
As $\quad \sigma=\sigma_0\left(1+\sqrt{\frac{r}{R}}\right)$
For magnetic induction due to entire disc, we integrate from $r=0$ to $r=R$
$\Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2} \int_0^n\left(1+\sqrt{\frac{r}{R}}\right) \cdot d r$
IInd Part
$$
\Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2}\left[r+\frac{2 r^{3 / 2}}{3 \sqrt{R}}\right]_0^R
$$
$$
\begin{aligned}
& \Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2}\left[R+\frac{2}{3} R\right] \\
& \Rightarrow \quad B=\frac{5}{6} \mu_0 \omega \sigma_0 R \Rightarrow \frac{B}{\mu_0 \omega \sigma_0 R}=\frac{5}{6}
\end{aligned}
$$

Charge on ring $d q=$ Area of ring $\times$ Charge density $\Rightarrow \quad d q=(2 \pi r \cdot d r) \sigma$
$\Rightarrow$ Current through ring, $d i=\frac{d q}{T}$, as angular velocity of disc is $\omega$.
So, $\quad \frac{2 \pi}{\omega}=T$
$\Rightarrow \quad d i=\frac{\omega d q}{2 \pi}=\frac{\omega(2 \pi r \cdot d r) \sigma}{2 \pi}=\omega r \sigma d r$
Now, magnetic induction due to elemental ring at the centre,
$$
d B=\frac{\mu_0 d i}{2 r}=\frac{\mu_0 \operatorname{\omega or} \sigma}{2 r} \cdot d r=\frac{\mu_0 \omega \sigma}{2} \cdot d r
$$
As $\quad \sigma=\sigma_0\left(1+\sqrt{\frac{r}{R}}\right)$
For magnetic induction due to entire disc, we integrate from $r=0$ to $r=R$
$\Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2} \int_0^n\left(1+\sqrt{\frac{r}{R}}\right) \cdot d r$
IInd Part
$$
\Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2}\left[r+\frac{2 r^{3 / 2}}{3 \sqrt{R}}\right]_0^R
$$
$$
\begin{aligned}
& \Rightarrow \quad B=\frac{\mu_0 \omega \sigma_0}{2}\left[R+\frac{2}{3} R\right] \\
& \Rightarrow \quad B=\frac{5}{6} \mu_0 \omega \sigma_0 R \Rightarrow \frac{B}{\mu_0 \omega \sigma_0 R}=\frac{5}{6}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.