Search any question & find its solution
Question:
Answered & Verified by Expert
A non-uniform bar of weight $W$ is suspended at rest by two strings of negligible weight as shown in the figure. The angles made by the strings with the vertical are $36.9^{\circ}$ and $53.1^{\circ}$ respectively. The bar is $2 \mathrm{~m}$ long. Calculate the distance ' $d$ ' of the centre of gravity of the bar from its left end.
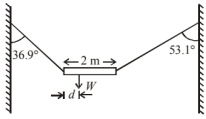

Solution:
1802 Upvotes
Verified Answer
Let $\theta_1=36.9^{\circ}$ and $\theta_2=53.1^{\circ}$
$T_1$ and $T_2$ are tensions in the two strings. For equilibrium of the rod along the horizontal,
$$
T_1 \sin \theta_1=T_2 \sin \theta_2
$$
$$
\frac{T_1}{T_2}=\frac{\sin \theta_2}{\sin \theta_1}=\frac{\sin 53.1^{\circ}}{\sin 36.9^{\circ}}=\frac{0.7407}{0.5477}=1.3523
$$
Let $C$ be the position of centre of gravity of the rod from the left and at a distance $d$.
For rotational equilibrium of the rod about $C$, the moment of the vertical forces must be equal and opposite.
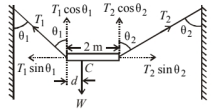
$$
\begin{aligned}
& T_1 \cos \theta_1 \times d=T_2 \cos \theta_2(2-d) \\
\Rightarrow & T_1 \cos 36.9^{\circ} \times d=T_2 \cos 53.1^{\circ}(2-d) \\
& \frac{T_1}{T_2} \times \frac{\cos 36.9^{\circ}}{\cos 53.1^{\circ}}=\frac{2-d}{d} \\
\Rightarrow & 1.3523 \times \frac{0.8366}{0.6718}=\frac{2}{d}-1 \\
& \frac{2}{d}=\frac{1.3523 \times 0.8366}{0.6718}+1 \Rightarrow d=0.745 \mathrm{~m}
\end{aligned}
$$
$T_1$ and $T_2$ are tensions in the two strings. For equilibrium of the rod along the horizontal,
$$
T_1 \sin \theta_1=T_2 \sin \theta_2
$$
$$
\frac{T_1}{T_2}=\frac{\sin \theta_2}{\sin \theta_1}=\frac{\sin 53.1^{\circ}}{\sin 36.9^{\circ}}=\frac{0.7407}{0.5477}=1.3523
$$
Let $C$ be the position of centre of gravity of the rod from the left and at a distance $d$.
For rotational equilibrium of the rod about $C$, the moment of the vertical forces must be equal and opposite.

$$
\begin{aligned}
& T_1 \cos \theta_1 \times d=T_2 \cos \theta_2(2-d) \\
\Rightarrow & T_1 \cos 36.9^{\circ} \times d=T_2 \cos 53.1^{\circ}(2-d) \\
& \frac{T_1}{T_2} \times \frac{\cos 36.9^{\circ}}{\cos 53.1^{\circ}}=\frac{2-d}{d} \\
\Rightarrow & 1.3523 \times \frac{0.8366}{0.6718}=\frac{2}{d}-1 \\
& \frac{2}{d}=\frac{1.3523 \times 0.8366}{0.6718}+1 \Rightarrow d=0.745 \mathrm{~m}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.