Search any question & find its solution
Question:
Answered & Verified by Expert
A parallel plate capacitor has the space between its plates filled by two slabs of thickness \( \frac{d}{2} \) each and dielectric constant \( K_{1} \) and \( K_{2} . d \) is the plate separation of the capacitor. The capacity of the capacitor is :
Options:
Solution:
1816 Upvotes
Verified Answer
The correct answer is:
\( \frac{2 \varepsilon_{0} A}{d}\left(\frac{K_{1} K_{2}}{K_{1}+K_{2}}\right) \)
Let us understand this such that two capacitors are connected in series with as dielectric constant of the dielectric mediums present in between the plates.
See the figure down below for better understanding.
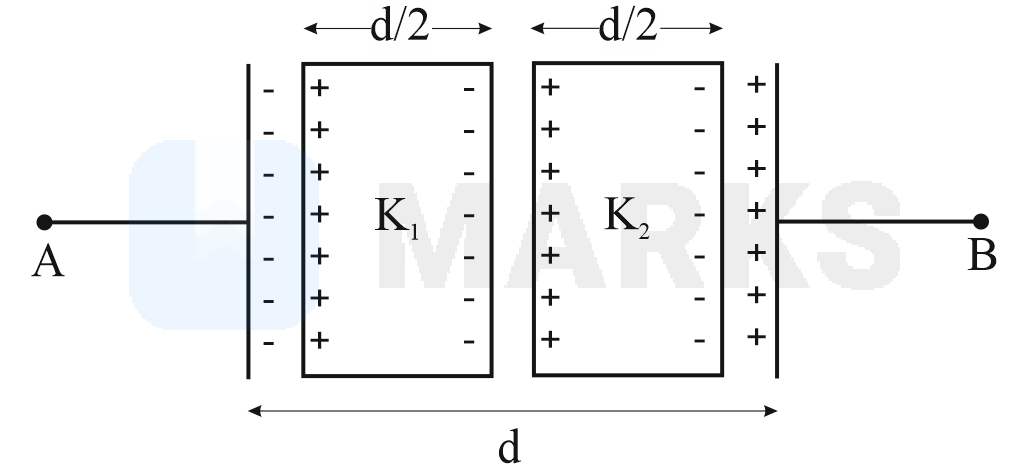
Now since both are arranged in series, we apply the formula for series combination of capacitor:
See the figure down below for better understanding.

Now since both are arranged in series, we apply the formula for series combination of capacitor:
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.