Search any question & find its solution
Question:
Answered & Verified by Expert
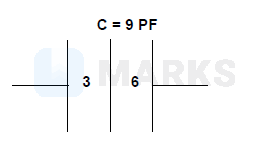
A parallel plate capacitor with air between the plates has a capacitance of $9 \mathrm{pF}$. The separation between its plates is ' $d$ '. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant $k_1=3$ and thickness $\frac{d}{3}$ while the other one has dielectric constant $\mathrm{k}_2=6$ and thickness $\frac{2 \mathrm{~d}}{3}$. Capacitance of the capacitor is now
Options:
Solution:
2125 Upvotes
Verified Answer
The correct answer is:
$40.5 \mathrm{pF}$
$40.5 \mathrm{pF}$
$$
\begin{aligned}
& C^{\prime}=\frac{A \varepsilon_0}{\frac{d_1}{3}+\frac{d_2}{6}}=\frac{A \varepsilon_0}{\frac{d}{9}+\frac{2 d}{18}}=\frac{18 A \varepsilon_0}{4 d} \\
& C^{\prime}=40.5 \mathrm{PF}
\end{aligned}
$$
\begin{aligned}
& C^{\prime}=\frac{A \varepsilon_0}{\frac{d_1}{3}+\frac{d_2}{6}}=\frac{A \varepsilon_0}{\frac{d}{9}+\frac{2 d}{18}}=\frac{18 A \varepsilon_0}{4 d} \\
& C^{\prime}=40.5 \mathrm{PF}
\end{aligned}
$$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.