Search any question & find its solution
Question:
Answered & Verified by Expert
A parallel plate capacitor with area $200 \mathrm{~cm}^2$ and separation between the plates $1.5 \mathrm{~cm}$, is connected across a battery of emf V. If the force of attraction between the plates is $25 \times 10^{-6} \mathrm{~N}$, the value of $V$ is approximately:
$$
\left.\left(\varepsilon_0=8.85 \times 10^{-12} \frac{\mathrm{C}^2}{\text { N.m }}\right)^2\right)
$$
Options:
$$
\left.\left(\varepsilon_0=8.85 \times 10^{-12} \frac{\mathrm{C}^2}{\text { N.m }}\right)^2\right)
$$
Solution:
2379 Upvotes
Verified Answer
The correct answer is:
$250 \mathrm{~V}$
$250 \mathrm{~V}$
Given area of Parallel plate capacitor, $A=$ $200 \mathrm{~cm}^2$
Separation between the plates, $d=1.5 \mathrm{~cm}$ Force of attraction between the plates, $F=$ $25 \times 10^{-6} \mathrm{~N}$ $F=Q E$
$F=\frac{Q^2}{2 A \epsilon_0} \quad$ (E due to parallel plate $\left.=\frac{\sigma}{2 \epsilon_0}=\frac{Q}{A 2 \epsilon_0}\right)$
But $Q=C V=\frac{\in_0 A(V)}{d}$
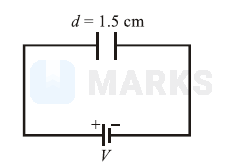
$$
\begin{gathered}
\left.\therefore F=\frac{\left(\epsilon_0 A V^2\right)}{\mathrm{d}^2 \times 2 \mathrm{~A} \epsilon_0}\right) \\
=\frac{\left(\epsilon_0 A\right)^2 \times V^2}{d^2 \times 2 \times\left(A \epsilon_0\right)}=\frac{\left(\epsilon_0 A\right) \times V^2}{d^2 \times 2} \\
\text { or, } 25 \times 10^{-6}=\frac{\left(8.85 \times 10^{-12}\right) \times\left(200 \times 10^{-4}\right) \times V^2}{2.25 \times 10^{-4} \times 2} \\
\Rightarrow V=\frac{25 \times 10^{-6} \times 2.25 \times 10^{-4} \times 2}{8.85 \times 10^{-12} \times 200 \times 10^{-4}} \approx 250 \mathrm{~V}
\end{gathered}
$$
Separation between the plates, $d=1.5 \mathrm{~cm}$ Force of attraction between the plates, $F=$ $25 \times 10^{-6} \mathrm{~N}$ $F=Q E$
$F=\frac{Q^2}{2 A \epsilon_0} \quad$ (E due to parallel plate $\left.=\frac{\sigma}{2 \epsilon_0}=\frac{Q}{A 2 \epsilon_0}\right)$
But $Q=C V=\frac{\in_0 A(V)}{d}$
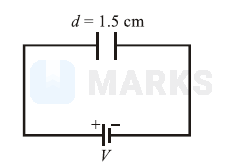
$$
\begin{gathered}
\left.\therefore F=\frac{\left(\epsilon_0 A V^2\right)}{\mathrm{d}^2 \times 2 \mathrm{~A} \epsilon_0}\right) \\
=\frac{\left(\epsilon_0 A\right)^2 \times V^2}{d^2 \times 2 \times\left(A \epsilon_0\right)}=\frac{\left(\epsilon_0 A\right) \times V^2}{d^2 \times 2} \\
\text { or, } 25 \times 10^{-6}=\frac{\left(8.85 \times 10^{-12}\right) \times\left(200 \times 10^{-4}\right) \times V^2}{2.25 \times 10^{-4} \times 2} \\
\Rightarrow V=\frac{25 \times 10^{-6} \times 2.25 \times 10^{-4} \times 2}{8.85 \times 10^{-12} \times 200 \times 10^{-4}} \approx 250 \mathrm{~V}
\end{gathered}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.