Search any question & find its solution
Question:
Answered & Verified by Expert
A paramagnetic sample shows a net magnetisation of 8 $\mathrm{Am}^{-1}$ when placed in an external magnetic field of $0.6 \mathrm{~T}$ at a temperature of $4 \mathrm{~K}$. When the same sample is placed in an external magnetic field of $0.2 \mathrm{~T}$ at a temperature of $16 \mathrm{~K}$, the magnetisation will be
Options:
Solution:
1960 Upvotes
Verified Answer
The correct answer is:
$\frac{2}{3} \mathrm{Am}^{-1}$
$\frac{2}{3} \mathrm{Am}^{-1}$
According to the Curie law, the intensity of magnetisation (I) is directly proportional to the magnetic field induction and inversely proportional to the temperature (t) in kelvin.
So, I magnetisation $\propto \frac{\mathrm{B} \text { (magnetic field induction) }}{\mathrm{t}(\text { temperature in kelvin) }}$
$$
\Rightarrow \quad \frac{\mathrm{I}_2}{\mathrm{I}_1}=\frac{\mathrm{B}_2}{\mathrm{~B}_1} \times \frac{\mathrm{t}_1}{\mathrm{t}_2}
$$
As given that $: I_1=8 \mathrm{Am}^{-1}, I_2=$ ?
$$
\begin{aligned}
&\mathrm{B}_1=0.6 \mathrm{~T}, \mathrm{t}_1=4 \mathrm{~K} \\
&\mathrm{~B}_2=0.2 \mathrm{~T}, \mathrm{t}_2=16 \mathrm{~K}
\end{aligned}
$$
by putting the value of $B_1, B_2, t_1, t_2 I_1$ in equation (i)
So, $\frac{0.2}{0.6} \times \frac{4}{16}=\frac{\mathrm{I}_2}{8}$
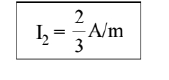
So, I magnetisation $\propto \frac{\mathrm{B} \text { (magnetic field induction) }}{\mathrm{t}(\text { temperature in kelvin) }}$
$$
\Rightarrow \quad \frac{\mathrm{I}_2}{\mathrm{I}_1}=\frac{\mathrm{B}_2}{\mathrm{~B}_1} \times \frac{\mathrm{t}_1}{\mathrm{t}_2}
$$
As given that $: I_1=8 \mathrm{Am}^{-1}, I_2=$ ?
$$
\begin{aligned}
&\mathrm{B}_1=0.6 \mathrm{~T}, \mathrm{t}_1=4 \mathrm{~K} \\
&\mathrm{~B}_2=0.2 \mathrm{~T}, \mathrm{t}_2=16 \mathrm{~K}
\end{aligned}
$$
by putting the value of $B_1, B_2, t_1, t_2 I_1$ in equation (i)
So, $\frac{0.2}{0.6} \times \frac{4}{16}=\frac{\mathrm{I}_2}{8}$
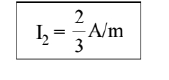
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.