Search any question & find its solution
Question:
Answered & Verified by Expert
A particle executing SHM along a straight line has zero velocity at points \(A\) and \(B\) whose distance from \(O\) on the same line \(O A B\) are \(a\) and \(b\), respectively. If the velocity at the mid point between \(A\) and \(B\) is \(v\), then its time period is
Options:
Solution:
1495 Upvotes
Verified Answer
The correct answer is:
\(\pi\left(\frac{b-a}{v}\right)\)
According to the question,
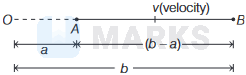
\(\therefore\) Amplitude
\(=\frac{\text { Distance travelled by the particles }}{2}(A \text { to } B)\)
Amplitude of particles executing simple harmonic motion (SHM) along a straight line \(A B\) is \((a)=\frac{b-a}{2}\).
Velocity of particle, \(v=\) Amplitude \(\times\) Oscillation frequency
\(\begin{aligned}
\therefore \quad v & =a \omega \\
v & =\left(\frac{b-a}{2}\right) \omega \text { or } \omega=\frac{2 v}{b-a} \quad \ldots (i)
\end{aligned}\)
\(\therefore\) Time period, \(T=\frac{2 \pi}{\omega}\)
Putting the value of \(\omega\) from Eq. (i) to above formula,
\(\Rightarrow \quad T=\frac{2 \pi}{2 v} \times(b-a) \Rightarrow T=\frac{b-a}{v} \pi\)
So, the time period of a particle executing SHM along a straight line from points \(A\) to \(B\) is,
\(T=\frac{b-a}{v} \pi\)
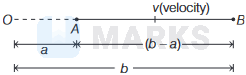
\(\therefore\) Amplitude
\(=\frac{\text { Distance travelled by the particles }}{2}(A \text { to } B)\)
Amplitude of particles executing simple harmonic motion (SHM) along a straight line \(A B\) is \((a)=\frac{b-a}{2}\).
Velocity of particle, \(v=\) Amplitude \(\times\) Oscillation frequency
\(\begin{aligned}
\therefore \quad v & =a \omega \\
v & =\left(\frac{b-a}{2}\right) \omega \text { or } \omega=\frac{2 v}{b-a} \quad \ldots (i)
\end{aligned}\)
\(\therefore\) Time period, \(T=\frac{2 \pi}{\omega}\)
Putting the value of \(\omega\) from Eq. (i) to above formula,
\(\Rightarrow \quad T=\frac{2 \pi}{2 v} \times(b-a) \Rightarrow T=\frac{b-a}{v} \pi\)
So, the time period of a particle executing SHM along a straight line from points \(A\) to \(B\) is,
\(T=\frac{b-a}{v} \pi\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.