Search any question & find its solution
Question:
Answered & Verified by Expert
A particle is describing simple harmonic motion. If its velocities are $v_1$ and $v_2$ when the displacements from the mean position are $y_1$ and $y_2$ respectively, then its time period is
Options:
Solution:
1776 Upvotes
Verified Answer
The correct answer is:
$2 \pi \sqrt{\frac{y_1^2-y_2^2}{v_2^2-v_1^2}}$
In simple harmonic motion, velocity $v=\omega \sqrt{A^2-y^2}$
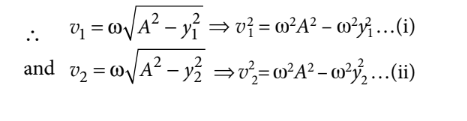
Solving equations (i) and (ii), we get
$\begin{aligned} & v_2^2-v_1^2=\omega^2\left(y_1^2-y_2^2\right) \\ & \omega=\sqrt{\frac{v_2^2-v_1^2}{y_1^2-y_2^2}}\end{aligned}$
$\Rightarrow T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{y_1^2-y_2^2}{v_2^2-v_1^2}}$
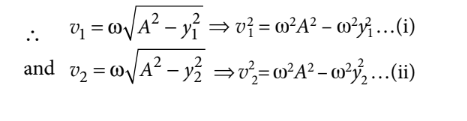
Solving equations (i) and (ii), we get
$\begin{aligned} & v_2^2-v_1^2=\omega^2\left(y_1^2-y_2^2\right) \\ & \omega=\sqrt{\frac{v_2^2-v_1^2}{y_1^2-y_2^2}}\end{aligned}$
$\Rightarrow T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{y_1^2-y_2^2}{v_2^2-v_1^2}}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.