Search any question & find its solution
Question:
Answered & Verified by Expert
A particle is executing SHM. The time taken for $\left(\frac{3}{8}\right)^{\text {th }}$ of oscillation from extreme positions is $x$. Then, the time taken for the particle to complete $\left(\frac{5}{8}\right)^{\text {th }}$ of oscillation from mean position is
Options:
Solution:
1305 Upvotes
Verified Answer
The correct answer is:
$\frac{7 x}{4}$
We divide total distance $4 A$ in 8 equal parts.
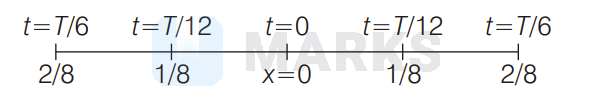
So, for a displacement of $\frac{3}{8}$ th of an oscillation from an extreme,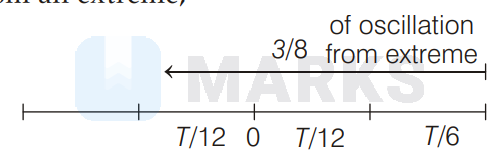
Time $=\frac{T}{6}+\frac{T}{12}+\frac{T}{12}=\frac{2+1+1}{12} T=\frac{4}{12} T=\frac{T}{3}$
Given, $\frac{T}{3}=x$ or $T=3 x$
Now, for $\frac{5}{8}$ th of oscillation from mean
$$
\text { Time }=\frac{T}{12}+\frac{T}{6}+\frac{T}{6}+\frac{T}{12}+\frac{T}{12}
$$
$\Rightarrow$ Time for $\frac{5}{8}$ th of oscillations
$$
=\frac{7}{12} T=\frac{7 \times 3 x}{12}=\frac{7}{4} x
$$
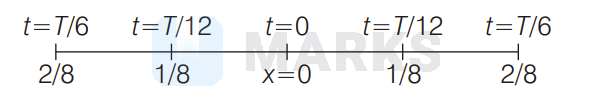
So, for a displacement of $\frac{3}{8}$ th of an oscillation from an extreme,
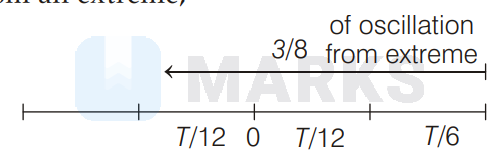
Time $=\frac{T}{6}+\frac{T}{12}+\frac{T}{12}=\frac{2+1+1}{12} T=\frac{4}{12} T=\frac{T}{3}$
Given, $\frac{T}{3}=x$ or $T=3 x$
Now, for $\frac{5}{8}$ th of oscillation from mean

$$
\text { Time }=\frac{T}{12}+\frac{T}{6}+\frac{T}{6}+\frac{T}{12}+\frac{T}{12}
$$
$\Rightarrow$ Time for $\frac{5}{8}$ th of oscillations
$$
=\frac{7}{12} T=\frac{7 \times 3 x}{12}=\frac{7}{4} x
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.