Search any question & find its solution
Question:
Answered & Verified by Expert
A particle is projected with a velocity \(v\) such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is \((g=\) acceleration due to gravity)
Options:
Solution:
2156 Upvotes
Verified Answer
The correct answer is:
\(\frac{4 v^2}{5 g}\)
Velocity of particle \(=v\)
If \(\theta\) is angle of projection such a way,
\(\begin{array}{ll}
& R=2 H \\
\Rightarrow & \frac{v^2 \sin 2 \theta}{g}=\frac{2 \cdot v^2 \sin ^2 \theta}{2 g} \\
& 2 \sin \theta \cos \theta=\sin ^2 \theta \\
\Rightarrow \quad & 2=\frac{\sin \theta}{\cos \theta} \Rightarrow 2=\tan \theta \Rightarrow \tan \theta=2
\end{array}\)
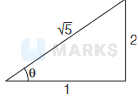
\(\begin{aligned} \therefore \quad & \sin \theta=\frac{2}{\sqrt{5}} \Rightarrow \cos \theta=\frac{1}{\sqrt{5}} \\ \therefore \quad \text { Range } & =\frac{v^2 \sin 2 \theta}{g}=\frac{v^2 \cdot 2 \sin \theta \cos \theta}{g} \\ & =\frac{v^2 \times 2 \times \frac{2}{\sqrt{5}} \times \frac{1}{\sqrt{5}}}{g}=\frac{4 v^2}{5 g}\end{aligned}\)
If \(\theta\) is angle of projection such a way,
\(\begin{array}{ll}
& R=2 H \\
\Rightarrow & \frac{v^2 \sin 2 \theta}{g}=\frac{2 \cdot v^2 \sin ^2 \theta}{2 g} \\
& 2 \sin \theta \cos \theta=\sin ^2 \theta \\
\Rightarrow \quad & 2=\frac{\sin \theta}{\cos \theta} \Rightarrow 2=\tan \theta \Rightarrow \tan \theta=2
\end{array}\)

\(\begin{aligned} \therefore \quad & \sin \theta=\frac{2}{\sqrt{5}} \Rightarrow \cos \theta=\frac{1}{\sqrt{5}} \\ \therefore \quad \text { Range } & =\frac{v^2 \sin 2 \theta}{g}=\frac{v^2 \cdot 2 \sin \theta \cos \theta}{g} \\ & =\frac{v^2 \times 2 \times \frac{2}{\sqrt{5}} \times \frac{1}{\sqrt{5}}}{g}=\frac{4 v^2}{5 g}\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.