The de-Broglie wavelength of the particle varies cyclically between two values $\lambda_1$ and $\lambda_2$, if is possible when if particle is moving in an elliptical orbit with origin as its one focus.
Consider the figure given below


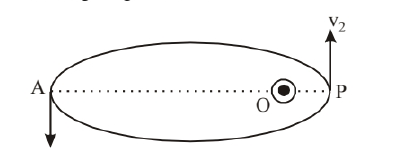
Let $v_1, v_2$ be the speed of particle at $A$ and $B$ respectively and origin is at $\mathrm{O}$. If $\lambda_1, \lambda_2$ are the de-Broglie wavelengths associated with particle while moving at A and B respectively. Then,
$$
\lambda_1=\frac{\mathrm{h}}{\mathrm{mv}_1} \text { and } \lambda_2=\frac{\mathrm{h}}{\mathrm{mv}_2}
$$

$$
\begin{aligned}
&\therefore \quad \frac{\lambda_1}{\lambda_2}=\frac{v_2}{v_1} \\
&\text { since }\left(\therefore \lambda_1>\lambda_2\right) \text { given } \\
&\therefore \quad v_2>v_1
\end{aligned}
$$
By law of conservation of angular momentum, the speed of the particle moves faster when it is closer to focus. From figure, we note that origin $\mathrm{O}$ is closed to $\mathrm{P}$ than $\mathrm{A}$. So, the object is close to $\mathrm{B}$ than $\mathrm{A}$ or the partice is nearer to the origin when wavelength is $\lambda_2$ then when wavelength is $\lambda_1$.