Search any question & find its solution
Question:
Answered & Verified by Expert
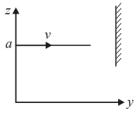
A particle of mass $m$ is moving in $y z$-plane with a uniform velocity $v$ with its trajectory running parallel to +ve $y$-axis and intersecting $z$-axis at $z=a$ in figure. The change in its angular momentum about the origin as it bounces elastically from a wall at $y=$ constant is
Options:

Solution:
1178 Upvotes
Verified Answer
The correct answer is:
$2 m v a \hat{e}_x$
$2 m v a \hat{e}_x$
The initial velocity is $v_i=v \hat{e}_y$ and after reflection from the wall, the final velocity is $v_f=-v \hat{e}_y$. The trajectory is at constant distance $a$ on $z$ axis and as particle moves along $y$ axis, its $y$ component changes.
So position vector (moving along $y$-axis),
$$
\vec{r}=y \hat{e}_y+a \hat{e}_z
$$
Hence, the change in angular momentum is
$$
\vec{r} \times m\left(v_f-v_j\right)=2 m v a \hat{e}_x
$$
So position vector (moving along $y$-axis),
$$
\vec{r}=y \hat{e}_y+a \hat{e}_z
$$
Hence, the change in angular momentum is
$$
\vec{r} \times m\left(v_f-v_j\right)=2 m v a \hat{e}_x
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.