Search any question & find its solution
Question:
Answered & Verified by Expert
A particle rotates in horizontal circle of radius 'R' in a conical funnel, with speed 'V'.
The inner surface of the funnel is smooth. The height of the plane of the circle from
the vertex of the funnel is $(\mathrm{g}=$ acceleration due to gravity $)$
Options:
The inner surface of the funnel is smooth. The height of the plane of the circle from
the vertex of the funnel is $(\mathrm{g}=$ acceleration due to gravity $)$
Solution:
2982 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{V}^{2}}{\mathrm{~g}}$
$\mathrm{mg}=\mathrm{R} \sin \theta$
$\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{R} \cos \theta$
$\tan \theta=\frac{\mathrm{rg}}{\mathrm{v}^{2}}$
$\tan \theta=\frac{\mathrm{r}}{\mathrm{h}}$
$\mathrm{h}=\frac{\mathrm{v}^{2}}{\mathrm{~g}}$
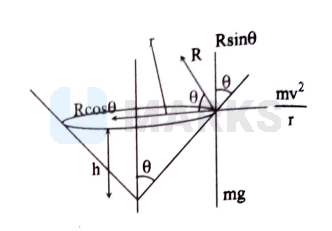
$\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{R} \cos \theta$
$\tan \theta=\frac{\mathrm{rg}}{\mathrm{v}^{2}}$
$\tan \theta=\frac{\mathrm{r}}{\mathrm{h}}$
$\mathrm{h}=\frac{\mathrm{v}^{2}}{\mathrm{~g}}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.