Search any question & find its solution
Question:
Answered & Verified by Expert
A person moves $30 \mathrm{~m}$ North and then $20 \mathrm{~m}$ towards East and finally $30 \sqrt{2} \mathrm{~m}$ in South-West direction. The displacement of the person from the origin will be
Options:
Solution:
1156 Upvotes
Verified Answer
The correct answer is:
$10 \mathrm{~m}$ along West
Let us use the conventional directions, as shown in figure, to solve this problem.
According to question, let us draw the diagram.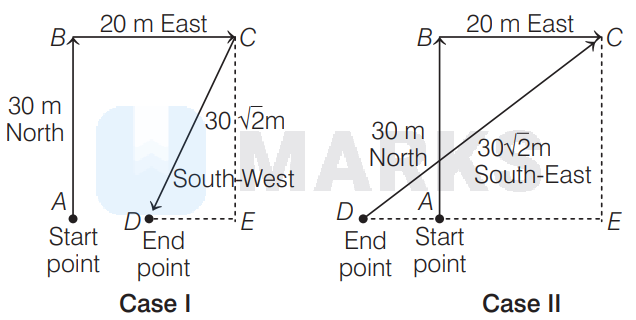
There are two possible diagrams.
Clearly, $\quad C E=A B=30 \mathrm{~m} \Rightarrow C D=30 \sqrt{2} \mathrm{~m}$
Using Pythagoras theorem,
$(C E)^2+(D E)^2=(C D)^2$
$\Rightarrow(D E)^2=(30 \sqrt{2})^2-(30)^2=1800-900=900 \mathrm{~m}$
$\Rightarrow \quad D E=30 \mathrm{~m}$
Now, it is clear that Case I is not possible.
Using Case II,
Clearly, displacement of the person is
End point - Start point $=D A$ (along West)
and $\quad D A=D E-A E$
$=30 \mathrm{~m}-20 \mathrm{~m}=10 \mathrm{~m} \quad$ (along West)

According to question, let us draw the diagram.

There are two possible diagrams.
Clearly, $\quad C E=A B=30 \mathrm{~m} \Rightarrow C D=30 \sqrt{2} \mathrm{~m}$
Using Pythagoras theorem,
$(C E)^2+(D E)^2=(C D)^2$
$\Rightarrow(D E)^2=(30 \sqrt{2})^2-(30)^2=1800-900=900 \mathrm{~m}$
$\Rightarrow \quad D E=30 \mathrm{~m}$
Now, it is clear that Case I is not possible.
Using Case II,
Clearly, displacement of the person is
End point - Start point $=D A$ (along West)
and $\quad D A=D E-A E$
$=30 \mathrm{~m}-20 \mathrm{~m}=10 \mathrm{~m} \quad$ (along West)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.