Search any question & find its solution
Question:
Answered & Verified by Expert
A plane EM wave travelling in vacuum along z-direction is given by $E=E_0 \sin (k z-\omega t) \hat{i}$ and $B=B_0 \sin (k z-\omega t) \hat{j}$.
(i) Evaluate $\int$ E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate $\int$ B.ds over the surface bounded by loop 1234
(iii) Use equation $\int E . d l=\frac{-d \phi_B}{d t}$ to prove $\frac{E_0}{B_0}=c$.
(iv) By using similar process and the equation
$$
\int \mathrm{B} . \mathrm{dl}=\mu_0 \mathrm{I}+\varepsilon_0 \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}, \text { prove that } \mathrm{c}=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}
$$
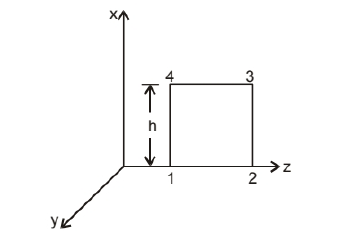
(i) Evaluate $\int$ E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate $\int$ B.ds over the surface bounded by loop 1234
(iii) Use equation $\int E . d l=\frac{-d \phi_B}{d t}$ to prove $\frac{E_0}{B_0}=c$.
(iv) By using similar process and the equation
$$
\int \mathrm{B} . \mathrm{dl}=\mu_0 \mathrm{I}+\varepsilon_0 \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}, \text { prove that } \mathrm{c}=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}
$$

Solution:
1647 Upvotes
Verified Answer
(i) $$
\text { According to the given figure }
$$
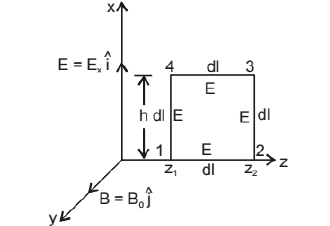
Let us consider the electromagnetic wave is propagating along z-axis, and electric field vector (E) be along $\mathrm{x}$-axis and magnetic field vector $B$ along $y$-axis. so, $E=$
$\mathrm{E}_0 \hat{\mathrm{i}}$ and $\mathrm{B}=\mathrm{B}_0 \hat{\mathrm{j}}$
Line integral of $E$ over the closed path 1234 in $x-z$ plane, shown in above figure.
$$
\text { So, } \begin{aligned}
\oint & E \cdot d l-\int_1^2 E \cdot d l+\int_2^3 E \cdot d l+\int_3^4 E \cdot d l+\int_4^1 E \cdot d l \\
&=\int_1^2 E \cdot d l \cos 90+\int_2^3 E \cdot d l \cos 0+\int_3^4 E \cdot d l \cos 90+\int_4^1 E \cdot d l \cos 180^{\circ} \\
&=E_0 \mathrm{~h}\left[\sin \left(k z_2-\omega \mathrm{t}\right)-\sin \left(k z_1-g \omega t\right)\right]
\end{aligned}
$$
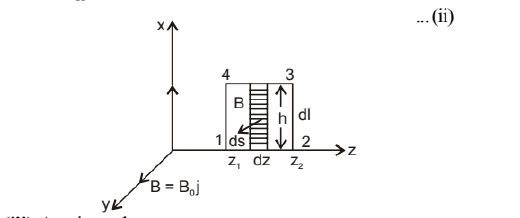
(ii) Now again let us consider the rectangle 1234 to be made of strips of area ds $=h d z$ each and the angle between $(d \overrightarrow{\mathrm{S}})$ and $(\overrightarrow{\mathrm{B}})$ is zero.
$$
\begin{aligned}
\text { So, } \quad \int \vec{B} \cdot \overrightarrow{d s} &=\int_{z_2} B \cdot d s \cos 0=\int B \cdot d s \\
&=\int_{Z_1}^{B_0} B_0 \sin (k z-\omega t) h d z \\
=\frac{-B_0 \mathrm{~h}}{\mathrm{k}}\left[\cos \left(k z_2-\omega t\right)-\cos \left(k z_1-\omega t\right)\right]
\end{aligned}
$$
(iii) As given that,
$$
\begin{aligned}
\oint E \cdot d l=\frac{-d \phi_B}{d t}=&-\frac{\mathrm{d}}{\mathrm{dt}} \oint \text { B.ds } \\
& {\left[\because B=B_0 \sin (k z-\omega \mathrm{t})\right] }
\end{aligned}
$$
Equating Eqs. (i) and (ii), we have
$$
\begin{aligned}
&=\frac{-\mathrm{d}}{\mathrm{dt}}\left[\frac{\mathrm{B}_0 \mathrm{~h}}{\mathrm{k}}\left\{\cos \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\cos \left(\mathrm{kz_{1 }}-\omega \mathrm{t}\right)\right\}\right] \\
&\mathrm{E}_0 \mathrm{~h}\left[\sin \left(\mathrm{kz} z_2-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz} z_1-\omega \mathrm{t}\right)\right] \\
&=\frac{\mathrm{B}_0 \mathrm{~h}}{\mathrm{k}} \omega\left[\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_1-\omega \mathrm{t}\right)\right] \\
&\text { So, } \mathrm{E}_0=\frac{\mathrm{B}_0 \omega}{\mathrm{k}}=\mathrm{B}_{\mathrm{y}} \mathrm{c}\left[\because \frac{\omega}{\mathrm{k}}=\mathrm{c}\right] \\
&\frac{E_0}{B_0}=c \\
&
\end{aligned}
$$
(iv) Let us consider a loop 1234 in y-z plane as shown in figure.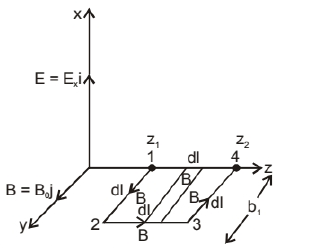
$$
\begin{aligned}
&\oint \mathrm{B} \cdot \mathrm{dl}=\int_1^2 \mathrm{~B} \cdot \mathrm{dl}+\int_2^3 \mathrm{~B} \cdot \mathrm{dl}+\int_3^4 \mathrm{~B} \cdot \mathrm{dl}+\int_4^1 \mathrm{~B} \cdot \mathrm{dl} \\
&=\int_1^2 \mathrm{~B} \mathrm{dl} \cos 0+\int_2^3 \mathrm{~B} \cdot \mathrm{dl} \cos 90^{\circ}+\int_3^4 \mathrm{~B} \mathrm{dl} \cos 180^{\circ} \\
&=\mathrm{B}_0 \mathrm{~h}\left[\sin \left(\mathrm{kz} \mathrm{p}_1-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)\right] \ldots \text { (iii) }\left[\because \mathrm{dl} \cos 90^{\circ}\right.
\end{aligned}
$$
Now to calculate $\phi_{\mathrm{e}}=\int$ E.ds, consider the rectangle strip of loop $1,2,3,4$ of area (ds) each (ds $=\mathrm{hdz})$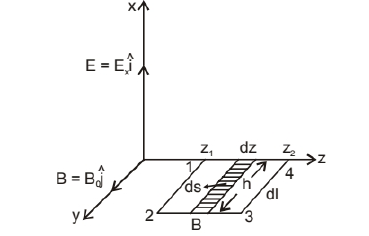
$$
\begin{aligned}
&\phi_{\mathrm{E}}=\int \mathrm{E} \cdot \mathrm{ds}=\int \mathrm{Eds} \cos 0^{\circ}=\int \mathrm{Eds} \\
&=\int_{z_1}^{z_2} \mathrm{E}_0 \sin \left(k z_1-\omega t\right) h d z \\
&\phi_{\mathrm{E}}=-\frac{\mathrm{E}_0 \mathrm{~h}}{\mathrm{k}}\left[\cos \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\cos \left(\mathrm{kz_{1 }}-\omega \mathrm{t}\right)\right] \\
&\therefore \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}=\frac{\mathrm{E}_0 \mathrm{~h} \omega}{\mathrm{k}}\left[\sin \left(\mathrm{kz}_1-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)\right] \\
&
\end{aligned}
$$
By applying ampere's law,
$$
\oint \text { B.dl }=\mu_0\left(I_c+\frac{\varepsilon_0 d \phi_{\mathrm{E}}}{\mathrm{dt}}\right)
$$
where, $I_c=$ conduction current For vacuum, $I_c=0$
So, $\quad \oint$ B.dl $=\mu_0 \varepsilon \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}$
From Eqs. (iii) and (iv) then we have,
$$
B_0 \mathrm{~h}\left[\sin \left(k z_1-\omega t\right) \sin \left(k z_2-\omega t\right)\right]
$$
$$
\begin{aligned}
\quad=\mu_0 \varepsilon_0 \frac{E_0 h \omega}{k}\left[\sin \left(k z_1-\omega t\right)-\sin \left(k z_2-\omega t\right)\right] \\
B_0=& E_0 \frac{\omega \mu_0 \varepsilon_0}{k}
\end{aligned}
$$
So, $\frac{E_0}{B_0} \frac{\omega}{k}=\frac{1}{\mu_0 \varepsilon_0} \quad\left(\therefore \frac{E_0}{B_0}=c\right.$ and $\left.\omega=\mathrm{ck}\right)$ then,
$$
\frac{\text { c.ck }}{\mathrm{k}}=\frac{1}{\mu_0 \varepsilon_0} \text { or } \mathrm{c}^2=\frac{1}{\mu_0 \varepsilon_0}
$$
Hence, $\quad \mathrm{c}=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}$
\text { According to the given figure }
$$

Let us consider the electromagnetic wave is propagating along z-axis, and electric field vector (E) be along $\mathrm{x}$-axis and magnetic field vector $B$ along $y$-axis. so, $E=$
$\mathrm{E}_0 \hat{\mathrm{i}}$ and $\mathrm{B}=\mathrm{B}_0 \hat{\mathrm{j}}$
Line integral of $E$ over the closed path 1234 in $x-z$ plane, shown in above figure.
$$
\text { So, } \begin{aligned}
\oint & E \cdot d l-\int_1^2 E \cdot d l+\int_2^3 E \cdot d l+\int_3^4 E \cdot d l+\int_4^1 E \cdot d l \\
&=\int_1^2 E \cdot d l \cos 90+\int_2^3 E \cdot d l \cos 0+\int_3^4 E \cdot d l \cos 90+\int_4^1 E \cdot d l \cos 180^{\circ} \\
&=E_0 \mathrm{~h}\left[\sin \left(k z_2-\omega \mathrm{t}\right)-\sin \left(k z_1-g \omega t\right)\right]
\end{aligned}
$$
(ii) Now again let us consider the rectangle 1234 to be made of strips of area ds $=h d z$ each and the angle between $(d \overrightarrow{\mathrm{S}})$ and $(\overrightarrow{\mathrm{B}})$ is zero.
$$
\begin{aligned}
\text { So, } \quad \int \vec{B} \cdot \overrightarrow{d s} &=\int_{z_2} B \cdot d s \cos 0=\int B \cdot d s \\
&=\int_{Z_1}^{B_0} B_0 \sin (k z-\omega t) h d z \\
=\frac{-B_0 \mathrm{~h}}{\mathrm{k}}\left[\cos \left(k z_2-\omega t\right)-\cos \left(k z_1-\omega t\right)\right]
\end{aligned}
$$

(iii) As given that,
$$
\begin{aligned}
\oint E \cdot d l=\frac{-d \phi_B}{d t}=&-\frac{\mathrm{d}}{\mathrm{dt}} \oint \text { B.ds } \\
& {\left[\because B=B_0 \sin (k z-\omega \mathrm{t})\right] }
\end{aligned}
$$
Equating Eqs. (i) and (ii), we have
$$
\begin{aligned}
&=\frac{-\mathrm{d}}{\mathrm{dt}}\left[\frac{\mathrm{B}_0 \mathrm{~h}}{\mathrm{k}}\left\{\cos \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\cos \left(\mathrm{kz_{1 }}-\omega \mathrm{t}\right)\right\}\right] \\
&\mathrm{E}_0 \mathrm{~h}\left[\sin \left(\mathrm{kz} z_2-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz} z_1-\omega \mathrm{t}\right)\right] \\
&=\frac{\mathrm{B}_0 \mathrm{~h}}{\mathrm{k}} \omega\left[\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_1-\omega \mathrm{t}\right)\right] \\
&\text { So, } \mathrm{E}_0=\frac{\mathrm{B}_0 \omega}{\mathrm{k}}=\mathrm{B}_{\mathrm{y}} \mathrm{c}\left[\because \frac{\omega}{\mathrm{k}}=\mathrm{c}\right] \\
&\frac{E_0}{B_0}=c \\
&
\end{aligned}
$$
(iv) Let us consider a loop 1234 in y-z plane as shown in figure.

$$
\begin{aligned}
&\oint \mathrm{B} \cdot \mathrm{dl}=\int_1^2 \mathrm{~B} \cdot \mathrm{dl}+\int_2^3 \mathrm{~B} \cdot \mathrm{dl}+\int_3^4 \mathrm{~B} \cdot \mathrm{dl}+\int_4^1 \mathrm{~B} \cdot \mathrm{dl} \\
&=\int_1^2 \mathrm{~B} \mathrm{dl} \cos 0+\int_2^3 \mathrm{~B} \cdot \mathrm{dl} \cos 90^{\circ}+\int_3^4 \mathrm{~B} \mathrm{dl} \cos 180^{\circ} \\
&=\mathrm{B}_0 \mathrm{~h}\left[\sin \left(\mathrm{kz} \mathrm{p}_1-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)\right] \ldots \text { (iii) }\left[\because \mathrm{dl} \cos 90^{\circ}\right.
\end{aligned}
$$
Now to calculate $\phi_{\mathrm{e}}=\int$ E.ds, consider the rectangle strip of loop $1,2,3,4$ of area (ds) each (ds $=\mathrm{hdz})$

$$
\begin{aligned}
&\phi_{\mathrm{E}}=\int \mathrm{E} \cdot \mathrm{ds}=\int \mathrm{Eds} \cos 0^{\circ}=\int \mathrm{Eds} \\
&=\int_{z_1}^{z_2} \mathrm{E}_0 \sin \left(k z_1-\omega t\right) h d z \\
&\phi_{\mathrm{E}}=-\frac{\mathrm{E}_0 \mathrm{~h}}{\mathrm{k}}\left[\cos \left(\mathrm{kz}_2-\omega \mathrm{t}\right)-\cos \left(\mathrm{kz_{1 }}-\omega \mathrm{t}\right)\right] \\
&\therefore \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}=\frac{\mathrm{E}_0 \mathrm{~h} \omega}{\mathrm{k}}\left[\sin \left(\mathrm{kz}_1-\omega \mathrm{t}\right)-\sin \left(\mathrm{kz}_2-\omega \mathrm{t}\right)\right] \\
&
\end{aligned}
$$
By applying ampere's law,
$$
\oint \text { B.dl }=\mu_0\left(I_c+\frac{\varepsilon_0 d \phi_{\mathrm{E}}}{\mathrm{dt}}\right)
$$
where, $I_c=$ conduction current For vacuum, $I_c=0$
So, $\quad \oint$ B.dl $=\mu_0 \varepsilon \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}$
From Eqs. (iii) and (iv) then we have,
$$
B_0 \mathrm{~h}\left[\sin \left(k z_1-\omega t\right) \sin \left(k z_2-\omega t\right)\right]
$$
$$
\begin{aligned}
\quad=\mu_0 \varepsilon_0 \frac{E_0 h \omega}{k}\left[\sin \left(k z_1-\omega t\right)-\sin \left(k z_2-\omega t\right)\right] \\
B_0=& E_0 \frac{\omega \mu_0 \varepsilon_0}{k}
\end{aligned}
$$
So, $\frac{E_0}{B_0} \frac{\omega}{k}=\frac{1}{\mu_0 \varepsilon_0} \quad\left(\therefore \frac{E_0}{B_0}=c\right.$ and $\left.\omega=\mathrm{ck}\right)$ then,
$$
\frac{\text { c.ck }}{\mathrm{k}}=\frac{1}{\mu_0 \varepsilon_0} \text { or } \mathrm{c}^2=\frac{1}{\mu_0 \varepsilon_0}
$$
Hence, $\quad \mathrm{c}=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.