The motion of the ball is shown below.



$$
\text { Range, } \begin{aligned}
R & =\frac{u^2 \sin 2 \theta}{g} \\
& =\frac{900 \sin (2 \times 30)}{10}=\frac{900 \times \sin 60^{\circ}}{10} \\
R & =\frac{900 \times \sqrt{3}}{10 \times 2}=\frac{900 \sqrt{3}}{20}=45 \sqrt{3} \mathrm{~m}
\end{aligned}
$$
Since, the IInd player is at $21 \sqrt{3} \mathrm{~m}$ in the direction of kick and he is running to catch the ball, so this can be represented as shown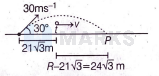


Let the man runs with speed $v$ towards point $P$ to catch the ball just at point $P$ before it touches the ground in the same time when ball reaches the point $P$.
The man will travel distance $=24 \sqrt{3} \mathrm{~m}$
$\Rightarrow$ Distance $=$ speed $\times$ time
$\Rightarrow \quad 2 u \sqrt{3}=v \times t$
Where, $t$ is the time of run as well as time of flight since both the ball and IInd man start running at same time hence $t=$ time of flight
We know that,
Time of flight, $t=\frac{2 u \sin \theta}{g}=\frac{2 \times 30 \times \sin 30^{\circ}}{10}$
$$
t=3 \mathrm{~s}
$$
Put $t=35$ in Eq. (i)
$$
\begin{aligned}
& & 2 u \sqrt{3} & =v \times 3 \\
\Rightarrow & & v & =8 \sqrt{3} \mathrm{~m} / \mathrm{s}
\end{aligned}
$$
Option (c) is the correct answer.