Search any question & find its solution
Question:
Answered & Verified by Expert
A point $P$ is moving in uniform circular motion with radius $3 \mathrm{~m}$. Let at some instant the acceleration of the point is $\mathbf{a}=(6 \hat{\mathbf{i}}-4 \hat{\mathbf{j}}) \mathrm{m} / \mathrm{s}^2$, the position vector is $\mathbf{r}$ and velocity vector is $\mathbf{v}$. Choose the correct statement.
Options:
Solution:
1787 Upvotes
Verified Answer
The correct answer is:
$v \cdot a=0$ and $r \times a=0$
The given situation is shown in the following figure
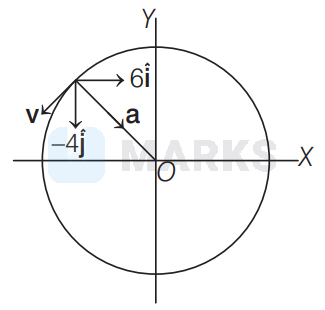
Acceleration, $\mathbf{a}=6 \hat{\mathbf{i}}-4 \hat{\mathbf{j}}$
Clearly, acceleration $\mathbf{a}$ is perpendicular to velocity $\mathbf{v}$, hence
$\mathbf{v} \cdot \mathbf{a}=0$
Again, position vector $\mathbf{r}$ is parallel to acceleration a, hence
$\mathbf{r} \times \mathbf{a}=0$

Acceleration, $\mathbf{a}=6 \hat{\mathbf{i}}-4 \hat{\mathbf{j}}$
Clearly, acceleration $\mathbf{a}$ is perpendicular to velocity $\mathbf{v}$, hence
$\mathbf{v} \cdot \mathbf{a}=0$
Again, position vector $\mathbf{r}$ is parallel to acceleration a, hence
$\mathbf{r} \times \mathbf{a}=0$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.