Search any question & find its solution
Question:
Answered & Verified by Expert
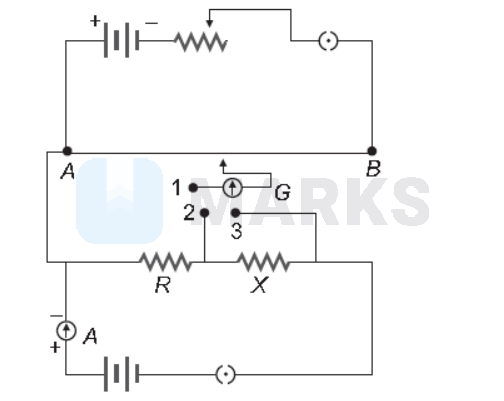
A potentiometer circuit is set up as shown. The potential gradient across the potentiometer wire, is $\mathrm{k}$ volt/cm and the ammeter, present in the circuit, reads 1.0 A when two way key is switched off. The balance points, when the key between the terminals (i) 1 and 2 (ii) 1 and 3 , is plugged in, are found to be at lengths $\mathrm{l}_1 \mathrm{~cm}$ and $\mathrm{l}_2 \mathrm{~cm}$ respectively. The magnitudes, of the resistors $\mathrm{R}$ and $\mathrm{X}$, in ohm, are then, equal, respectively, to
Options:

Solution:
2961 Upvotes
Verified Answer
The correct answer is:
$\mathrm{kl}_1$ and $\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)$
The balancing length for $\mathrm{R}$ (when 1,2 are connected) be is $l_1$ and balancing length for $\mathrm{R}+\mathrm{X}$ (when 1,3 is connected is $\mathrm{l}_2$ )
Then $\quad \mathrm{iR}=\mathrm{kl}_1$
and $\mathrm{i}(\mathrm{R}+\mathrm{X})=\mathrm{kl}_2$
Given $\quad \mathrm{i}=1 \mathrm{~A}$
$$
\begin{array}{r}
\mathrm{R}=\mathrm{kl}_1 \\
\mathrm{R}+\mathrm{X}=\mathrm{kl}_2
\end{array}
$$
Subtracting Eq. (i) from Eq. (ii), we get
$$
\mathrm{X}=\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)
$$
Then $\quad \mathrm{iR}=\mathrm{kl}_1$
and $\mathrm{i}(\mathrm{R}+\mathrm{X})=\mathrm{kl}_2$
Given $\quad \mathrm{i}=1 \mathrm{~A}$
$$
\begin{array}{r}
\mathrm{R}=\mathrm{kl}_1 \\
\mathrm{R}+\mathrm{X}=\mathrm{kl}_2
\end{array}
$$
Subtracting Eq. (i) from Eq. (ii), we get
$$
\mathrm{X}=\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.