Search any question & find its solution
Question:
Answered & Verified by Expert
A random variable $X$ has the following probability distribution:
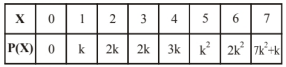
Determine
$\begin{array}{ll}\text { (i) } k & \text { (ii) } \mathbf{P}(\mathrm{X} < 3)\end{array}$
(iii) $\mathrm{P}(\mathrm{X}>6) \quad$ (iv) $\mathrm{P}(0 < X < 3)$

Determine
$\begin{array}{ll}\text { (i) } k & \text { (ii) } \mathbf{P}(\mathrm{X} < 3)\end{array}$
(iii) $\mathrm{P}(\mathrm{X}>6) \quad$ (iv) $\mathrm{P}(0 < X < 3)$
Solution:
2578 Upvotes
Verified Answer
(i) Sum of probabilities $=1$
i.e., $0+k+2 k+2 k+3 k+2 k^2+7 k^2+k=1$
$10 \mathrm{k}^2+9 \mathrm{k}=1$ or $10 \mathrm{k}^2+9 \mathrm{k}-1=0$
$(k+1)(10 k-1)=0, \quad k=-1$ or $k=\frac{1}{10}$
$$
\mathrm{k} \neq-1 \quad \therefore \mathrm{k}=\frac{1}{10}
$$
$\therefore \quad$ The probability distribution is
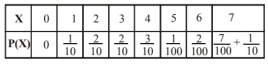
(ii) $\mathrm{P}(\mathrm{X} < 3)=\mathrm{P}(0)+\mathrm{P}(1)+\mathrm{P}(2)=0$
$$
+\frac{1}{10}+\frac{2}{10}=\frac{3}{10}
$$
(iii) $\mathrm{P}(\mathrm{X}>6)=\mathrm{P}(7)=\frac{7}{100}+\frac{1}{10}=\frac{7+10}{100}=\frac{17}{100}$
(iv) $\mathrm{P}(0 < \mathrm{X} < 3)=\mathrm{P}(1)+\mathrm{P}(2)=\frac{1}{10}+\frac{2}{10}=\frac{3}{10}$
i.e., $0+k+2 k+2 k+3 k+2 k^2+7 k^2+k=1$
$10 \mathrm{k}^2+9 \mathrm{k}=1$ or $10 \mathrm{k}^2+9 \mathrm{k}-1=0$
$(k+1)(10 k-1)=0, \quad k=-1$ or $k=\frac{1}{10}$
$$
\mathrm{k} \neq-1 \quad \therefore \mathrm{k}=\frac{1}{10}
$$
$\therefore \quad$ The probability distribution is

(ii) $\mathrm{P}(\mathrm{X} < 3)=\mathrm{P}(0)+\mathrm{P}(1)+\mathrm{P}(2)=0$
$$
+\frac{1}{10}+\frac{2}{10}=\frac{3}{10}
$$
(iii) $\mathrm{P}(\mathrm{X}>6)=\mathrm{P}(7)=\frac{7}{100}+\frac{1}{10}=\frac{7+10}{100}=\frac{17}{100}$
(iv) $\mathrm{P}(0 < \mathrm{X} < 3)=\mathrm{P}(1)+\mathrm{P}(2)=\frac{1}{10}+\frac{2}{10}=\frac{3}{10}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.