Search any question & find its solution
Question:
Answered & Verified by Expert
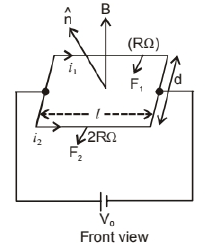
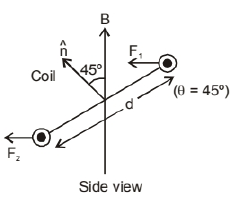
A rectangular conducting loop consists of two wires on two opposite sides of length $l$ joined together by rods of length $\mathrm{d}$. The wires are each of the same material but with cross-sections differing by a factor of 2 . The thicker wire has a resistance $R$ and the rods are of low resistance, which in turn are connected to a constant voltage source $\mathrm{V}_0$. The loop is placed in uniform a magnetic field $B$ at $45^{\circ}$ to its plane. Find $\tau$, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.
Solution:
2755 Upvotes
Verified Answer
As we know that $\mathrm{R}=\rho l / \mathrm{A}$, consider the thicker wire has a resistance $R$ then the thinner wire has a resistance $2 R$ as the wires are of the same material and same length but
$$
\text { with cross-sections differing by a factor } 2 \text { is given. }
$$
By Ohm's law
$$
(\mathrm{V}=\mathrm{IR}) \quad\left(\because \mathrm{V}_1=\mathrm{V}_2=\mathrm{V}_0\right)
$$
So, for current $\left(\mathrm{I}_1\right)=\frac{\mathrm{V}_1}{\mathrm{R}_1}=\frac{\mathrm{V}_0}{R}$ and for current $\left(\mathrm{I}_2\right)=\frac{\mathrm{V}_2}{\mathrm{R}_2}=\frac{\mathrm{V}_0}{2 \mathrm{R}}$ Now, the force and torque on first wire is
$$
\begin{aligned}
&F_1=i_1 I B \sin 45^{\circ} \\
&F_1=\frac{V_0}{R} \frac{I B}{\sqrt{2}} \\
&\tau_1=(d) \cdot F_1=\frac{V_0 l d B}{\sqrt{2} R}
\end{aligned}
$$
Similarly, the force and torque on thinner wire is
$$
\mathrm{F}_2 \mathrm{i}_2 1 \mathrm{~B} \sin 45^{\circ}=\frac{\mathrm{V}_0}{2 \mathrm{R}} \frac{1 \mathrm{~B}}{\sqrt{2}}
$$
$$
\tau_2=F_2=\frac{V_0 l d B}{2 \sqrt{2} R}
$$
Hence resultant torque is $\tau=\tau_1-\tau_2$
$$
\tau=\frac{1}{2 \sqrt{2}} \frac{\mathrm{V}_0 \mathrm{ldB}}{\mathrm{R}}
$$
$$
\text { with cross-sections differing by a factor } 2 \text { is given. }
$$


By Ohm's law
$$
(\mathrm{V}=\mathrm{IR}) \quad\left(\because \mathrm{V}_1=\mathrm{V}_2=\mathrm{V}_0\right)
$$
So, for current $\left(\mathrm{I}_1\right)=\frac{\mathrm{V}_1}{\mathrm{R}_1}=\frac{\mathrm{V}_0}{R}$ and for current $\left(\mathrm{I}_2\right)=\frac{\mathrm{V}_2}{\mathrm{R}_2}=\frac{\mathrm{V}_0}{2 \mathrm{R}}$ Now, the force and torque on first wire is
$$
\begin{aligned}
&F_1=i_1 I B \sin 45^{\circ} \\
&F_1=\frac{V_0}{R} \frac{I B}{\sqrt{2}} \\
&\tau_1=(d) \cdot F_1=\frac{V_0 l d B}{\sqrt{2} R}
\end{aligned}
$$
Similarly, the force and torque on thinner wire is
$$
\mathrm{F}_2 \mathrm{i}_2 1 \mathrm{~B} \sin 45^{\circ}=\frac{\mathrm{V}_0}{2 \mathrm{R}} \frac{1 \mathrm{~B}}{\sqrt{2}}
$$
$$
\tau_2=F_2=\frac{V_0 l d B}{2 \sqrt{2} R}
$$
Hence resultant torque is $\tau=\tau_1-\tau_2$
$$
\tau=\frac{1}{2 \sqrt{2}} \frac{\mathrm{V}_0 \mathrm{ldB}}{\mathrm{R}}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.