Search any question & find its solution
Question:
Answered & Verified by Expert
A resistor of resistance $R$, capacitor of capacitance $C$ and inductor of inductance $L$ are connected in parallel to AC power source of voltage $\varepsilon_{0} \sin \omega t$. The maximum current through the resistance is half of the maximum current through the power source. Then value of $\mathrm{R}$ is
Options:
Solution:
2492 Upvotes
Verified Answer
The correct answer is:
$\frac{\sqrt{3}}{\left|\omega C-\frac{1}{\omega L}\right|}$
$\frac{i_{R_{0}}}{\sqrt{\left(i_{R_{0}}\right)^{2}+\left(i_{c_{0}}-i_{L_{0}}\right)^{2}}}=\frac{1}{2}$
$\Rightarrow \frac{\varepsilon_{0} / R}{\sqrt{\left(\varepsilon_{0} / R\right)^{2}+\left(\varepsilon_{0} \omega C-\frac{\varepsilon_{0}}{\omega L}\right)^{2}}}=\frac{1}{2}$
$\Rightarrow R=\frac{\sqrt{3}}{\left(\omega C-\frac{1}{\omega L}\right)}$
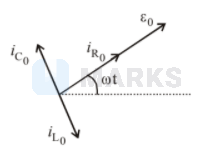
$\Rightarrow \frac{\varepsilon_{0} / R}{\sqrt{\left(\varepsilon_{0} / R\right)^{2}+\left(\varepsilon_{0} \omega C-\frac{\varepsilon_{0}}{\omega L}\right)^{2}}}=\frac{1}{2}$
$\Rightarrow R=\frac{\sqrt{3}}{\left(\omega C-\frac{1}{\omega L}\right)}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.