Search any question & find its solution
Question:
Answered & Verified by Expert
A rod of length $12 \mathrm{~cm}$ moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point $P$ on the rod, which is $3 \mathrm{~cm}$ from the end in contact with the $\mathrm{x}$-axis.
Solution:
1179 Upvotes
Verified Answer
Let $\mathrm{AB}=12 \mathrm{~cm}$ is the rod and $\mathrm{P}(x, y)$ is point on the rod such that
$P A=3 \mathrm{~cm} \quad \therefore \mathrm{PB}=9 \mathrm{~cm}$
Draw $\mathrm{PQ} \perp \mathrm{OB}$ and $\mathrm{PR} \perp \mathrm{OR}$
Let $\mathrm{BQ}=b$ and $\mathrm{AR}=a$
then from similar $\Delta s, \mathrm{BQP}$ and $\mathrm{PRA}$,
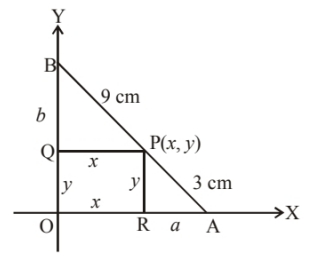
$\frac{b}{9}=\frac{y}{3}$ and $\frac{a}{3}=\frac{x}{9} \quad \therefore b=3 y$ and $a=\frac{1}{3} x$
$\begin{aligned}
\therefore \quad \mathrm{OA} &=x+a=x+\frac{x}{3}=\frac{4 x}{3} \\
\mathrm{OB}=y+b &=y+3 y=4 y
\end{aligned}$
Using, $\mathrm{OA}^2+\mathrm{OB}^2=\mathrm{AB}^2$, we have
$\frac{16}{9} x^2+16 y^2=144 \Rightarrow \frac{x^2}{81}+\frac{y^2}{9}=1$ which is locus of $\mathrm{P}$.
$P A=3 \mathrm{~cm} \quad \therefore \mathrm{PB}=9 \mathrm{~cm}$
Draw $\mathrm{PQ} \perp \mathrm{OB}$ and $\mathrm{PR} \perp \mathrm{OR}$
Let $\mathrm{BQ}=b$ and $\mathrm{AR}=a$
then from similar $\Delta s, \mathrm{BQP}$ and $\mathrm{PRA}$,

$\frac{b}{9}=\frac{y}{3}$ and $\frac{a}{3}=\frac{x}{9} \quad \therefore b=3 y$ and $a=\frac{1}{3} x$
$\begin{aligned}
\therefore \quad \mathrm{OA} &=x+a=x+\frac{x}{3}=\frac{4 x}{3} \\
\mathrm{OB}=y+b &=y+3 y=4 y
\end{aligned}$
Using, $\mathrm{OA}^2+\mathrm{OB}^2=\mathrm{AB}^2$, we have
$\frac{16}{9} x^2+16 y^2=144 \Rightarrow \frac{x^2}{81}+\frac{y^2}{9}=1$ which is locus of $\mathrm{P}$.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.