Search any question & find its solution
Question:
Answered & Verified by Expert
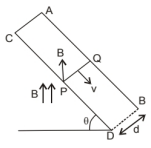
A rod of mass $m$ and resistance $R$ slides smoothly over two parallel perfectly conducting wires kept sloping at an angle 0 with respect to the horizontal (figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field $\mathrm{B}$ along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

Solution:
2286 Upvotes
Verified Answer
From free body diagram the component of magnetic field (B) perpendicular the plan (PQ) $=\mathrm{B} \cos \theta$
Now, the conductor moves with speed v perpendicular to $\operatorname{B} \cos \theta$ component of magnetic field.
So, $\quad \mathrm{d} \phi=\vec{B} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}$
$\mathrm{d} \phi=(\operatorname{B} \cos \theta)(\mathrm{d} \times \mathrm{v} \times \mathrm{dt})$
$\left(\frac{d \phi}{d t}=v B d \cos \theta\right)$
This causes motional emf across two ends of rod, which is given $b y=v(B \cos \theta) d$
$$
\left(\therefore \frac{\mathrm{d} \phi}{\mathrm{dt}}=\mathrm{iR}\right)
$$
So that it makes flow of induced current
$$
\mathrm{i}=\frac{\mathrm{v}(\mathrm{B} \cos \theta) \mathrm{d}}{\mathrm{R}}
$$
where, $R$ is the resistance of rod. Now, current carrying rod experience force $F=i B d$, (horizontally in backward direction). So, the component of magnetic force parallel to incline plane along upward direction
$$
\begin{aligned}
&=\mathrm{F} \cos \theta=\mathrm{iBd} \cos \theta \\
\mathrm{F}_{\mathrm{m}} &=\left(\frac{\mathrm{v}(\mathrm{B} \cos \theta) \mathrm{d}}{\mathrm{R}}\right) \mathrm{Bd} \cos \theta
\end{aligned}
$$
Also, the component of weight (mg) parallel to incline plane along downward direction $=m g \sin \theta$.
From Newton's second law of motion
$$
\begin{aligned}
\mathrm{m} \frac{\mathrm{d}^2 \mathrm{x}}{\mathrm{dt}^2} &=\mathrm{mg} \sin \theta-\mathrm{F}_{\mathrm{m}} \\
\mathrm{m} \frac{\mathrm{d}^2 \mathrm{x}}{\mathrm{dt}^2}=\mathrm{mg} \sin \theta &-\frac{\mathrm{vB} \cos \theta \mathrm{d}}{\mathrm{R}} \times(\mathrm{Bd}) \cos \theta \\
\frac{\mathrm{dv}}{\mathrm{dt}} &=\mathrm{g} \sin \theta-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}(\cos \theta)^2 \mathrm{v}
\end{aligned}
$$
$$
\frac{\mathrm{dv}}{\mathrm{dt}}+\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}(\cos \theta)^2 \mathrm{v}=\mathrm{g} \sin \theta
$$
Which is the linear differential equation.
After solving the equation we have,
$$
\mathrm{v}=\frac{\mathrm{g} \sin \theta}{\frac{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}{\mathrm{mR}}}+\operatorname{Aexp}\left(-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}\left(\cos ^2 \theta\right) \mathrm{t}\right)
$$
Where, $\mathrm{A}$ is a constant to be determine by initial conditions, at, $\quad t=0, \quad v=0$
We have $\quad 0=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}-\mathrm{Ae}^0$
$$
\Rightarrow \quad \mathrm{A}=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}
$$
By putting the value of $A$ in equation (i), Then the required expression of velocity as a function of time is
$$
\mathrm{v}=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}\left(1-\exp \left(-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}\left(\cos ^2 \theta\right) \mathrm{t}\right)\right)
$$
Let us consider a new constant $(\alpha)$ is
$$
=\left(\frac{\mathrm{mR}}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}\right)
$$
So, $\mathrm{v}=\alpha \mathrm{g} \sin \theta\left(1-\mathrm{e}^{-t / \alpha}\right)$
Now, the conductor moves with speed v perpendicular to $\operatorname{B} \cos \theta$ component of magnetic field.
So, $\quad \mathrm{d} \phi=\vec{B} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}$
$\mathrm{d} \phi=(\operatorname{B} \cos \theta)(\mathrm{d} \times \mathrm{v} \times \mathrm{dt})$
$\left(\frac{d \phi}{d t}=v B d \cos \theta\right)$
This causes motional emf across two ends of rod, which is given $b y=v(B \cos \theta) d$
$$
\left(\therefore \frac{\mathrm{d} \phi}{\mathrm{dt}}=\mathrm{iR}\right)
$$
So that it makes flow of induced current
$$
\mathrm{i}=\frac{\mathrm{v}(\mathrm{B} \cos \theta) \mathrm{d}}{\mathrm{R}}
$$
where, $R$ is the resistance of rod. Now, current carrying rod experience force $F=i B d$, (horizontally in backward direction). So, the component of magnetic force parallel to incline plane along upward direction
$$
\begin{aligned}
&=\mathrm{F} \cos \theta=\mathrm{iBd} \cos \theta \\
\mathrm{F}_{\mathrm{m}} &=\left(\frac{\mathrm{v}(\mathrm{B} \cos \theta) \mathrm{d}}{\mathrm{R}}\right) \mathrm{Bd} \cos \theta
\end{aligned}
$$
Also, the component of weight (mg) parallel to incline plane along downward direction $=m g \sin \theta$.
From Newton's second law of motion
$$
\begin{aligned}
\mathrm{m} \frac{\mathrm{d}^2 \mathrm{x}}{\mathrm{dt}^2} &=\mathrm{mg} \sin \theta-\mathrm{F}_{\mathrm{m}} \\
\mathrm{m} \frac{\mathrm{d}^2 \mathrm{x}}{\mathrm{dt}^2}=\mathrm{mg} \sin \theta &-\frac{\mathrm{vB} \cos \theta \mathrm{d}}{\mathrm{R}} \times(\mathrm{Bd}) \cos \theta \\
\frac{\mathrm{dv}}{\mathrm{dt}} &=\mathrm{g} \sin \theta-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}(\cos \theta)^2 \mathrm{v}
\end{aligned}
$$
$$
\frac{\mathrm{dv}}{\mathrm{dt}}+\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}(\cos \theta)^2 \mathrm{v}=\mathrm{g} \sin \theta
$$
Which is the linear differential equation.
After solving the equation we have,
$$
\mathrm{v}=\frac{\mathrm{g} \sin \theta}{\frac{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}{\mathrm{mR}}}+\operatorname{Aexp}\left(-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}\left(\cos ^2 \theta\right) \mathrm{t}\right)
$$
Where, $\mathrm{A}$ is a constant to be determine by initial conditions, at, $\quad t=0, \quad v=0$
We have $\quad 0=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}-\mathrm{Ae}^0$
$$
\Rightarrow \quad \mathrm{A}=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}
$$
By putting the value of $A$ in equation (i), Then the required expression of velocity as a function of time is
$$
\mathrm{v}=\frac{\mathrm{mgR} \sin \theta}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}\left(1-\exp \left(-\frac{\mathrm{B}^2 \mathrm{~d}^2}{\mathrm{mR}}\left(\cos ^2 \theta\right) \mathrm{t}\right)\right)
$$
Let us consider a new constant $(\alpha)$ is
$$
=\left(\frac{\mathrm{mR}}{\mathrm{B}^2 \mathrm{~d}^2 \cos ^2 \theta}\right)
$$
So, $\mathrm{v}=\alpha \mathrm{g} \sin \theta\left(1-\mathrm{e}^{-t / \alpha}\right)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.