Search any question & find its solution
Question:
Answered & Verified by Expert
A rope of mass $5 \mathrm{~kg}$ is hanging between two supports as shown. The tension at the lowest point of the rope is close to $\left(\right.$ take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$ )
Options:
Solution:
2869 Upvotes
Verified Answer
The correct answer is:
$14 \mathrm{~N}$
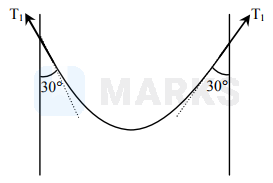
$\therefore 2 \mathrm{~T}_{1} \cos 30^{\circ}=\mathrm{mg}=5 \times 10=50$
$2 \mathrm{~T}_{1} \cos 30^{\circ}=50$
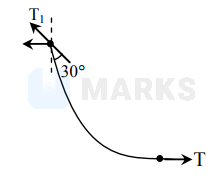
$\begin{aligned} \mathrm{T} &=\mathrm{T}_{1} \sin 30^{\circ} \\ &=\frac{50}{\frac{2 \sqrt{3}}{2}} \cdot \frac{1}{2}=\frac{25}{\sqrt{3}}=\frac{25 \sqrt{3}}{3} \\ \mathrm{~T} &=14.41 \mathrm{~N} \end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.