Search any question & find its solution
Question:
Answered & Verified by Expert
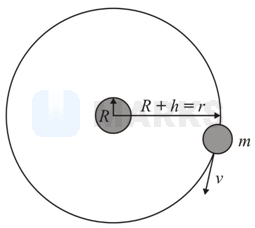
A satellite is revolving in circular orbit of radius \( r \) around the earth of mass \( M \). Time of revolution of satellite is
Options:
Solution:
1506 Upvotes
Verified Answer
The correct answer is:
\( T \propto \sqrt{\frac{r^{3}}{G M}} \)
When the satellite is moving in circular orbit after launching the satellite, then centripetal force should be equal to the gravitational force,
where are universal gravitational constant, the mass of the planet, the mass of satellite and height where the satellite is projected,
Now the time period of the satellite,
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.