Search any question & find its solution
Question:
Answered & Verified by Expert
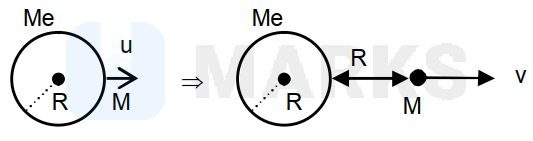
A satellite of mass \( M \) is launched vertically upwards with an initial speed \( u \) from the surface of the earth. After it reaches height \( R \) ( \( R= \) radius of the earth), it ejects a rocket of mass \( \frac{M}{10} \) so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is ( \( G \) is the gravitational constant; \( M_{e} \) is the mass of the earth):
Options:
Solution:
1017 Upvotes
Verified Answer
The correct answer is:
\( 5 M\left(u^{2}-\frac{119}{200} \frac{G M_{e}}{R}\right) \)
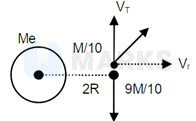
Transverse velocity of rocket
Radial velocity of rocket
Kinetic energy
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.