Search any question & find its solution
Question:
Answered & Verified by Expert
(a) Show that for a projectile the angle between the velocity and the $x$-axis as a function of time is given by
$$
\boldsymbol{\theta}(t)=\tan ^{-1}\left(\frac{v_{o y}-g t}{v_{o x}}\right)
$$
(b) Show that the projection angle $\theta_0$ for a projectile launched from the origin is given by
$$
\theta_0=\tan ^{-1}\left(\frac{4 h_m}{R}\right)
$$
where the symbols have their usual meaning.
$$
\boldsymbol{\theta}(t)=\tan ^{-1}\left(\frac{v_{o y}-g t}{v_{o x}}\right)
$$
(b) Show that the projection angle $\theta_0$ for a projectile launched from the origin is given by
$$
\theta_0=\tan ^{-1}\left(\frac{4 h_m}{R}\right)
$$
where the symbols have their usual meaning.
Solution:
2722 Upvotes
Verified Answer
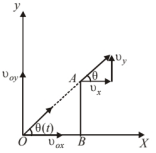
(a) Let a projectile fired at an angle $\theta$ with $x$-axis.
As $\theta$ depends on $t, \theta(t)$, at any instant
$$
\tan \theta(t)=\frac{v_y}{v_x}=\frac{v_{o y}-g t}{v_{o x}}
$$
(Since, $v_y=v_{o y}-g t$ and $v_x=v_{o x}$ )
$$
\Rightarrow \theta(t)=\tan ^{-1}\left(\frac{v_{o y}-g t}{v_{\alpha x}}\right)
$$
(b) Since, $h_{\max }=\frac{u^2 \sin ^2 \theta}{2 g}$ and $R=\frac{u^2 \sin ^2 \theta}{g}$
$$
\Rightarrow \frac{h_{\max }}{R}=\frac{\frac{u^2 \sin ^2 \theta}{2 g}}{\frac{u^2 \sin 2 \theta}{g}}
$$
$$
\begin{aligned}
&=\frac{\tan \theta}{4}(\text { As } \sin 2 \theta=2 \sin \theta \cos \theta) \\
\Rightarrow \quad \frac{\tan \theta}{4} &=\frac{h_{\max }}{R}
\end{aligned}
$$
or $\tan \theta=\frac{4 h_{\max }}{R}$ or $\theta=\tan ^{-1}\left(\frac{4 h_{\max }}{R}\right)$
As $\theta$ depends on $t, \theta(t)$, at any instant
$$
\tan \theta(t)=\frac{v_y}{v_x}=\frac{v_{o y}-g t}{v_{o x}}
$$
(Since, $v_y=v_{o y}-g t$ and $v_x=v_{o x}$ )
$$
\Rightarrow \theta(t)=\tan ^{-1}\left(\frac{v_{o y}-g t}{v_{\alpha x}}\right)
$$
(b) Since, $h_{\max }=\frac{u^2 \sin ^2 \theta}{2 g}$ and $R=\frac{u^2 \sin ^2 \theta}{g}$
$$
\Rightarrow \frac{h_{\max }}{R}=\frac{\frac{u^2 \sin ^2 \theta}{2 g}}{\frac{u^2 \sin 2 \theta}{g}}
$$
$$
\begin{aligned}
&=\frac{\tan \theta}{4}(\text { As } \sin 2 \theta=2 \sin \theta \cos \theta) \\
\Rightarrow \quad \frac{\tan \theta}{4} &=\frac{h_{\max }}{R}
\end{aligned}
$$

or $\tan \theta=\frac{4 h_{\max }}{R}$ or $\theta=\tan ^{-1}\left(\frac{4 h_{\max }}{R}\right)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.