Search any question & find its solution
Question:
Answered & Verified by Expert
A simple harmonic progressive wave is given by $\mathrm{y}=\mathrm{y}_0 \sin 2 \pi\left(\mathrm{nt}-\frac{\mathrm{x}}{\lambda}\right)$. If the wave velocity is $\left(\frac{1}{8}\right)^{\mathrm{th}}$ the maximum particle velocity then the wavelength is
Options:
Solution:
1203 Upvotes
Verified Answer
The correct answer is:
$\frac{\pi \mathrm{y}_0}{4}$
Given wave equation $\mathrm{y}=\mathrm{y}_0 \sin \pi\left(\mathrm{nt}-\frac{\mathrm{x}}{\lambda}\right)$
$\therefore$ Particle velocity $=\frac{\mathrm{dy}}{\mathrm{dt}}=\left(\mathrm{y}_0 \pi \mathrm{n}\right) \cos \pi\left(\mathrm{nt}-\frac{\mathrm{x}}{\lambda}\right)$
If the wave velocity is $\left(\frac{1}{8}\right)^{\text {th }}$ of the maximum particle velocity, then,
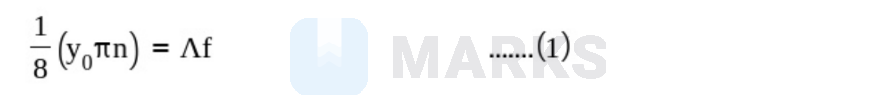
Where $\Lambda$ is the wavelength and $\mathrm{f}$ is the frequency. Frequency is given by
$f=\frac{\omega}{2 \pi}=\frac{\pi n}{2 \pi}=\frac{n}{2}$
Therefore, by plugging $\mathrm{f}$ into equation (1), we get the wavelength:
$\Lambda=\frac{2 \pi y_0}{8}=\frac{\pi y_0}{4}$
$\therefore$ Particle velocity $=\frac{\mathrm{dy}}{\mathrm{dt}}=\left(\mathrm{y}_0 \pi \mathrm{n}\right) \cos \pi\left(\mathrm{nt}-\frac{\mathrm{x}}{\lambda}\right)$
If the wave velocity is $\left(\frac{1}{8}\right)^{\text {th }}$ of the maximum particle velocity, then,
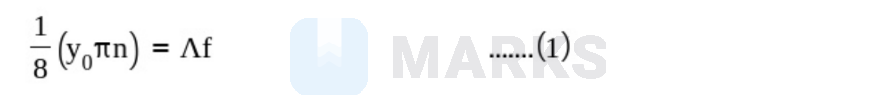
Where $\Lambda$ is the wavelength and $\mathrm{f}$ is the frequency. Frequency is given by
$f=\frac{\omega}{2 \pi}=\frac{\pi n}{2 \pi}=\frac{n}{2}$
Therefore, by plugging $\mathrm{f}$ into equation (1), we get the wavelength:
$\Lambda=\frac{2 \pi y_0}{8}=\frac{\pi y_0}{4}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.