Search any question & find its solution
Question:
Answered & Verified by Expert
A simple pendulum has length $2 \mathrm{~m}$ and a bob of mass 100 gram. It is whirled in a horizontal plane. If the string breaks under a tension of $10 \mathrm{~N}$, the angle made by the string with vertical is $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)$
Options:
Solution:
1029 Upvotes
Verified Answer
The correct answer is:
$\cos ^{-1}(0 \cdot 1)$
A simple pendulum has a length of $2 \mathrm{~m}$ and a bob of mass of $100\mathrm{~grams}$. It is whirled in a horizontal plane. If the string breaks under a tension of $10 \mathrm{~N}$, the angle made by the string with vertical is $\cos ^{-1}(0.1)$.
$\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$
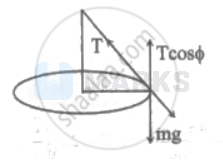
$\mathrm{L}=2 \mathrm{~m}$
$\mathrm{~m}=\frac{100}{1000}=0.1 \mathrm{~kg}$
$\operatorname{Tcos} \Phi=m g$
$\operatorname{Tsin} \Phi=\frac{m v^{2}}{R}$
$\cos \Phi=\frac{m g}{T}=\frac{0.1 \times 10}{10}=0.1$
$\therefore \Phi=\cos ^{-1}(0.1)$
$\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$

$\mathrm{L}=2 \mathrm{~m}$
$\mathrm{~m}=\frac{100}{1000}=0.1 \mathrm{~kg}$
$\operatorname{Tcos} \Phi=m g$
$\operatorname{Tsin} \Phi=\frac{m v^{2}}{R}$
$\cos \Phi=\frac{m g}{T}=\frac{0.1 \times 10}{10}=0.1$
$\therefore \Phi=\cos ^{-1}(0.1)$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.