Search any question & find its solution
Question:
Answered & Verified by Expert
A simple pendulum of length ' $\ell$ ' has a bob of mass 'm'. It executes S.H.M. of small amplitude 'A'. The maximum tension in the string is
$(\mathrm{g}=$ acceleration due to gravity)
Options:
$(\mathrm{g}=$ acceleration due to gravity)
Solution:
1603 Upvotes
Verified Answer
The correct answer is:
$\operatorname{mg}\left(\frac{\mathrm{A}^{2}}{\ell^{2}}+1\right)$
(D)
$\begin{array}{l}
\mathrm{y}=\mathrm{A} \sin \omega \mathrm{t} \\
\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \\
\frac{2 \pi}{\mathrm{T}}=\sqrt{\frac{\mathrm{g}}{\ell}}=\omega
\end{array}$
$\begin{aligned}
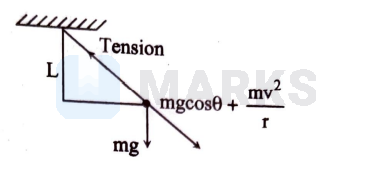
\therefore \text { Tension } &=m g \cos \theta+\frac{m v^{2}}{L} \\
T_{\max } &=m g+\frac{m v^{2}}{L} \quad \cos \theta=1 \\
&=m g\left(1+\frac{v^{2}}{g L}\right)
\end{aligned}$
Now, $y=A \sin \omega t$
$\begin{aligned} & \frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{A} \omega \cos \omega \mathrm{t} \\ &\left.\frac{\mathrm{dy}}{\mathrm{dt}}\right|_{\max }=\mathrm{A} \omega=\mathrm{A} \sqrt{\frac{\mathrm{g}}{\ell}}=\mathrm{V}_{\max } \\ \therefore & \mathrm{V}_{\max }^{2}=\mathrm{A}^{2} \frac{\mathrm{g}}{\mathrm{L}} \\ \therefore & \mathrm{T}_{\max }=\mathrm{mg}\left(1+\frac{\mathrm{A}^{2} \mathrm{~g}}{\mathrm{~L}^{2} \mathrm{~g}}\right)=\mathrm{mg}\left(1+\frac{\mathrm{A}^{2}}{\mathrm{~L}^{2}}\right) \end{aligned}$
$\begin{array}{l}
\mathrm{y}=\mathrm{A} \sin \omega \mathrm{t} \\
\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \\
\frac{2 \pi}{\mathrm{T}}=\sqrt{\frac{\mathrm{g}}{\ell}}=\omega
\end{array}$
$\begin{aligned}
\therefore \text { Tension } &=m g \cos \theta+\frac{m v^{2}}{L} \\
T_{\max } &=m g+\frac{m v^{2}}{L} \quad \cos \theta=1 \\
&=m g\left(1+\frac{v^{2}}{g L}\right)
\end{aligned}$
Now, $y=A \sin \omega t$
$\begin{aligned} & \frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{A} \omega \cos \omega \mathrm{t} \\ &\left.\frac{\mathrm{dy}}{\mathrm{dt}}\right|_{\max }=\mathrm{A} \omega=\mathrm{A} \sqrt{\frac{\mathrm{g}}{\ell}}=\mathrm{V}_{\max } \\ \therefore & \mathrm{V}_{\max }^{2}=\mathrm{A}^{2} \frac{\mathrm{g}}{\mathrm{L}} \\ \therefore & \mathrm{T}_{\max }=\mathrm{mg}\left(1+\frac{\mathrm{A}^{2} \mathrm{~g}}{\mathrm{~L}^{2} \mathrm{~g}}\right)=\mathrm{mg}\left(1+\frac{\mathrm{A}^{2}}{\mathrm{~L}^{2}}\right) \end{aligned}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.