Search any question & find its solution
Question:
Answered & Verified by Expert
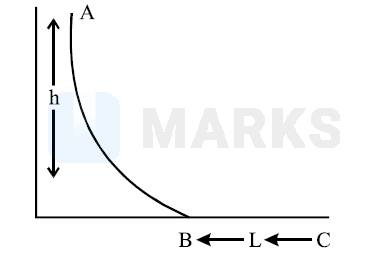
A small ball of mass $\mathrm{m}$ starts at a point $\mathrm{A}$ with speed $\mathrm{v}_{\mathrm{o}}$ and moves along a frictionless track $\mathrm{AB}$ as shown. The track $\mathrm{BC}$ has coefficient of friction $\mu$. The ball comes to stop at $\mathrm{C}$ after travelling a distance $L$ which is:
Options:

Solution:
2715 Upvotes
Verified Answer
The correct answer is:
$\frac{\mathrm{h}}{\mu}+\frac{\mathrm{v}_0^2}{2 \mu \mathrm{g}}$
$\frac{\mathrm{h}}{\mu}+\frac{\mathrm{v}_0^2}{2 \mu \mathrm{g}}$
Initial speed at point A, $u=v_0$
Speed at point $\mathrm{B}, v=$ ?
$$
\begin{aligned}
&v^2-u^2=2 g h \\
&v^2=v_0^2+2 g h
\end{aligned}
$$
Let ball travels distance ' $S$ ' before coming to rest
$$
\begin{aligned}
&S=\frac{v^2}{2 \mu g}=\frac{v_0^2+2 g h}{2 \mu g} \\
&=\frac{v_0^2}{2 \mu g}+\frac{2 g h}{2 \mu g}=\frac{h}{\mu}+\frac{v_0^2}{2 \mu g}
\end{aligned}
$$
Speed at point $\mathrm{B}, v=$ ?
$$
\begin{aligned}
&v^2-u^2=2 g h \\
&v^2=v_0^2+2 g h
\end{aligned}
$$
Let ball travels distance ' $S$ ' before coming to rest
$$
\begin{aligned}
&S=\frac{v^2}{2 \mu g}=\frac{v_0^2+2 g h}{2 \mu g} \\
&=\frac{v_0^2}{2 \mu g}+\frac{2 g h}{2 \mu g}=\frac{h}{\mu}+\frac{v_0^2}{2 \mu g}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.