Search any question & find its solution
Question:
Answered & Verified by Expert
A small block starts sliding down an inclined plane forming an angle $45^{\circ}$ horizontal. The coefficient of friction $\mu$, varies with distance $s$ as $\mu=c s^2$ where, $c$ is a constant of appropriate dimensions, then distance covered by the block before it stops is
Options:
Solution:
1283 Upvotes
Verified Answer
The correct answer is:
$\sqrt{\frac{3}{C}}$
$$
\text { Given that, }
$$
$\mu=C s^2 \quad\{\because s=$ distance and $C=$ constant $\}$
Net force on the block is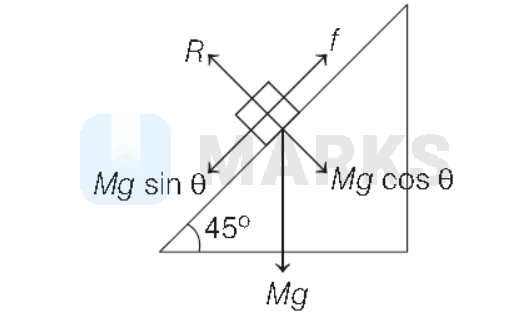
$$
\begin{gathered}
M g \sin \theta-f=M a \\
M g \sin \theta-\mu M g \cos \theta=M a \\
g \sin \theta-\mu g \cos \theta=a \\
g\left[\sin \theta-C s^2 \cos \theta\right]=a \\
a=\frac{d v}{d t}=v \frac{d v}{d s} \\
\because \quad a d s=v d v
\end{gathered}
$$
From Eqs. (i) and (ii), we get
$$
\Rightarrow \quad g\left[\sin \theta-C s^2 \cos \theta\right] d s=v d v
$$
Integrating both sides, we get
$$
\Rightarrow \quad(g \sin \theta) s-g \frac{C s^3}{3} \cos \theta=\frac{v^2}{2}+K
$$
For $\theta=45^{\circ}$, we have,
$$
\left(\frac{g}{\sqrt{2}}\right) s-\left(\frac{C s^3}{3}\right) \frac{g}{\sqrt{2}}=\frac{v^2}{2}+K
$$
Initially $t=0, s=0, u=0$, substituting these, we get $k=0$
So,
$$
\text { So, } \quad \begin{aligned}
& \frac{g}{\sqrt{2}}\left(s-\frac{C s^3}{3}\right) & =\frac{v^2}{2} \\
\Rightarrow & s-\frac{C s^3}{3} & =\frac{v^2}{2} \times \frac{\sqrt{2}}{g}
\end{aligned}
$$
The body stops, when $v=0 \Rightarrow s-\frac{C s^3}{3}=0$
$$
\Rightarrow \quad s=\frac{C s^3}{3} \Rightarrow s=\sqrt{\frac{3}{C}}
$$
\text { Given that, }
$$

$\mu=C s^2 \quad\{\because s=$ distance and $C=$ constant $\}$
Net force on the block is

$$
\begin{gathered}
M g \sin \theta-f=M a \\
M g \sin \theta-\mu M g \cos \theta=M a \\
g \sin \theta-\mu g \cos \theta=a \\
g\left[\sin \theta-C s^2 \cos \theta\right]=a \\
a=\frac{d v}{d t}=v \frac{d v}{d s} \\
\because \quad a d s=v d v
\end{gathered}
$$
From Eqs. (i) and (ii), we get
$$
\Rightarrow \quad g\left[\sin \theta-C s^2 \cos \theta\right] d s=v d v
$$
Integrating both sides, we get
$$
\Rightarrow \quad(g \sin \theta) s-g \frac{C s^3}{3} \cos \theta=\frac{v^2}{2}+K
$$
For $\theta=45^{\circ}$, we have,
$$
\left(\frac{g}{\sqrt{2}}\right) s-\left(\frac{C s^3}{3}\right) \frac{g}{\sqrt{2}}=\frac{v^2}{2}+K
$$
Initially $t=0, s=0, u=0$, substituting these, we get $k=0$
So,
$$
\text { So, } \quad \begin{aligned}
& \frac{g}{\sqrt{2}}\left(s-\frac{C s^3}{3}\right) & =\frac{v^2}{2} \\
\Rightarrow & s-\frac{C s^3}{3} & =\frac{v^2}{2} \times \frac{\sqrt{2}}{g}
\end{aligned}
$$
The body stops, when $v=0 \Rightarrow s-\frac{C s^3}{3}=0$
$$
\Rightarrow \quad s=\frac{C s^3}{3} \Rightarrow s=\sqrt{\frac{3}{C}}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.