Search any question & find its solution
Question:
Answered & Verified by Expert
A small wooden cube is placed on a plank. The plank performs a vertical S.H.M of frequency $\frac{3}{\pi} \mathrm{Hz}$. The maximum amplitude of the plank so that the wooden block does not leave the plank is [take $g=10 \mathrm{~m} / \mathrm{s}^2$ ]
Options:
Solution:
2606 Upvotes
Verified Answer
The correct answer is:
$\frac{5}{18} \mathrm{~m}$
Concept: wooden cube can leave the plank at the top extreme location when the plank just begins to move towards the equilibrium position. See the figure below:
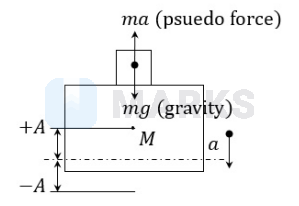
For cube not to leave plank the weight of the block should be more than the pseudo force on the cube:
$\text { ma } \leq \mathrm{mg}$
Therefore, $\mathrm{a} \leq \mathrm{g}$.
$|a|=\omega^2 x$ when, $x=A$ the amplitude
$\therefore \omega^2 \mathrm{~A} \leq \mathrm{g} \text { or } \mathrm{A} \leq \frac{\mathrm{g}}{\omega^2}$
Given, $\mathrm{f}=\frac{3}{\pi} \mathrm{Hz} \frac{\omega}{2 \pi}=\frac{1}{\mathrm{~T}}$
$\Rightarrow \omega=6 \mathrm{~Hz}$
$A \leq \frac{10}{6^2} \mathrm{~m}$
$\mathrm{A} \leq \frac{5}{18} \mathrm{~m}$

For cube not to leave plank the weight of the block should be more than the pseudo force on the cube:
$\text { ma } \leq \mathrm{mg}$
Therefore, $\mathrm{a} \leq \mathrm{g}$.
$|a|=\omega^2 x$ when, $x=A$ the amplitude
$\therefore \omega^2 \mathrm{~A} \leq \mathrm{g} \text { or } \mathrm{A} \leq \frac{\mathrm{g}}{\omega^2}$
Given, $\mathrm{f}=\frac{3}{\pi} \mathrm{Hz} \frac{\omega}{2 \pi}=\frac{1}{\mathrm{~T}}$
$\Rightarrow \omega=6 \mathrm{~Hz}$
$A \leq \frac{10}{6^2} \mathrm{~m}$
$\mathrm{A} \leq \frac{5}{18} \mathrm{~m}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.