Search any question & find its solution
Question:
Answered & Verified by Expert
A solid sphere and a hollow sphere of the same material and of a same size can be distinguished without weighing
Options:
Solution:
1907 Upvotes
Verified Answer
The correct answer is:
by rolling them simultaneously on an inclined plane
The acceleration of a body rolling down the plane $=a$.
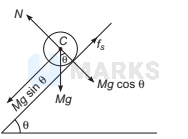
$\therefore \quad a=\frac{g \sin \theta}{1+\frac{K^2}{R^2}}$
where $K$ is radius of gyration and $R$ the radius of sphere.
For solid sphere,
$\frac{K^2}{R^2}=\frac{2}{5}$
$\therefore \quad a=\frac{5}{7} g \sin \theta$
$=0.7(g \sin \theta)$
For hollow sphere,
$\frac{K^2}{R^2}=\frac{2}{3}$
$=\frac{3}{5} g \sin \theta$
$=0.6(g \sin \theta)$
Since, acceleration of solid sphere is more than of hollow sphere, it rolls faster, and reaches the bottom of the inclined plane earlier.
Hence, solid sphere and hollow sphere can be distinguished by rolling them simultaneously on an inclined plane.

$\therefore \quad a=\frac{g \sin \theta}{1+\frac{K^2}{R^2}}$
where $K$ is radius of gyration and $R$ the radius of sphere.
For solid sphere,
$\frac{K^2}{R^2}=\frac{2}{5}$
$\therefore \quad a=\frac{5}{7} g \sin \theta$
$=0.7(g \sin \theta)$
For hollow sphere,
$\frac{K^2}{R^2}=\frac{2}{3}$
$=\frac{3}{5} g \sin \theta$
$=0.6(g \sin \theta)$
Since, acceleration of solid sphere is more than of hollow sphere, it rolls faster, and reaches the bottom of the inclined plane earlier.
Hence, solid sphere and hollow sphere can be distinguished by rolling them simultaneously on an inclined plane.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.