Search any question & find its solution
Question:
Answered & Verified by Expert
A solid sphere has mass ' $M$ ' and radius ' $R$ '. Its moment of inertia about a parallel axis passing through a point at a distance $\frac{R}{2}$ from its centre is
Options:
Solution:
1083 Upvotes
Verified Answer
The correct answer is:
$\frac{13 \mathrm{MR}^2}{20}$
Concept: Parallel axis theorem application.
The moment of inertia for a sphere about the central rotation axis is:
$\mathrm{I}_{\text {sphere }}=\frac{2}{5} \mathrm{MR}^2$
See the diagram below,
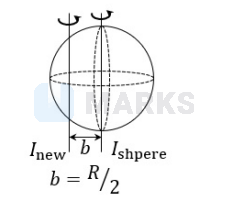
To find the moment of inertia about the new rotation axis we use parallel axis theorem: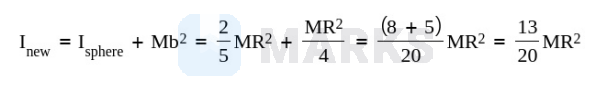
The moment of inertia for a sphere about the central rotation axis is:
$\mathrm{I}_{\text {sphere }}=\frac{2}{5} \mathrm{MR}^2$
See the diagram below,

To find the moment of inertia about the new rotation axis we use parallel axis theorem:
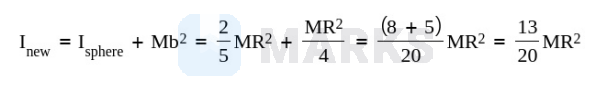
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.