Search any question & find its solution
Question:
Answered & Verified by Expert
A source of sound S emitting waves of frequency $100 \mathrm{~Hz}$ and an observor $\mathrm{O}$ are located at some distance from each other. The source is moving with a speed of $19.4 \mathrm{~ms}^{-1}$ at an angle of $60^{\circ}$ with the source observer line as shown in the figure. The observor is at rest. The apparent frequency observed by the observer is (velocity of sound in air $330 \mathrm{~ms}^{-1}$ )
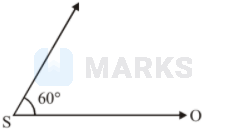
Options:

Solution:
2018 Upvotes
Verified Answer
The correct answer is:
$103 \mathrm{~Hz}$
Here, original frequency of sound, $\mathrm{f}_{0}=100 \mathrm{~Hz}$ Speed of source $V_{s}=19.4 \cos 60^{\circ}=9.7$
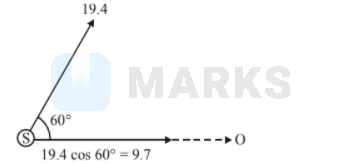
From Doppler's formula
$\mathrm{f}^{\mathrm{l}}=\mathrm{f}_{0}\left(\frac{\mathrm{V}-\mathrm{V}_{0}}{\mathrm{~V}-\mathrm{V}_{\mathrm{s}}}\right)$
$\mathrm{f}^{\mathrm{l}}=100\left(\frac{\mathrm{V}-0}{\mathrm{~V}-(+9.7)}\right)$
$\mathrm{f}^{\mathrm{l}}=100 \frac{\mathrm{V}}{\mathrm{V}\left(1-\frac{9.7}{\mathrm{~V}}\right)}$
$\mathrm{f}^{1}=100\left(1+\frac{9.7}{330}\right)=103 \mathrm{~Hz}$
Apparent frequency $\mathrm{f}^{1}=103 \mathrm{~Hz}$
From Doppler's formula
$\mathrm{f}^{\mathrm{l}}=\mathrm{f}_{0}\left(\frac{\mathrm{V}-\mathrm{V}_{0}}{\mathrm{~V}-\mathrm{V}_{\mathrm{s}}}\right)$
$\mathrm{f}^{\mathrm{l}}=100\left(\frac{\mathrm{V}-0}{\mathrm{~V}-(+9.7)}\right)$
$\mathrm{f}^{\mathrm{l}}=100 \frac{\mathrm{V}}{\mathrm{V}\left(1-\frac{9.7}{\mathrm{~V}}\right)}$
$\mathrm{f}^{1}=100\left(1+\frac{9.7}{330}\right)=103 \mathrm{~Hz}$
Apparent frequency $\mathrm{f}^{1}=103 \mathrm{~Hz}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.